题目内容
4.如果集合A={x|ax2+2x+1=0}中只有一个元素,则a的值是( )| A. | 0 | B. | 0 或1 | C. | 1 | D. | 0 或1或-1 |
分析 当a=0,x=-$\frac{1}{2}$,满足条件.当 a≠0,由△=0,求得a=1.综合可得a的值.
解答 解:当a=0,x=-$\frac{1}{2}$,满足条件.
当 a≠0,由△=22-4a=0,则得a=1.
所以当a=0,或a=1时,A只有一个元素.
故选B.
点评 本题主要考查集合关系中参数的取值范围问题,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
9.若点P(1,-2)位于角α终边上,则sin2α+2cos2α=( )
| A. | -$\frac{14}{5}$ | B. | -$\frac{7}{5}$ | C. | -2 | D. | $\frac{4}{5}$ |
2.已知函数f(x)=x3-3x,则函数h(x)=f[f(x)]-c,c∈[-2,2]的零点个数( )
| A. | 5或6个 | B. | 3或9个 | C. | 9或10个 | D. | 5或9个 |
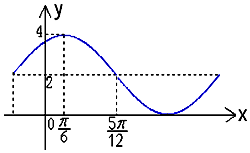 函数f(x)=Asin(ωx+ϕ)+B的一部分图象如图所示,其中A>0,ω>0,|φ|<$\frac{π}{2}$.
函数f(x)=Asin(ωx+ϕ)+B的一部分图象如图所示,其中A>0,ω>0,|φ|<$\frac{π}{2}$. 已知正方形ADEF所在平面与等腰梯形BCEF所在平面互相垂直,且BC=2BF=2EF=4,G为BC中点.
已知正方形ADEF所在平面与等腰梯形BCEF所在平面互相垂直,且BC=2BF=2EF=4,G为BC中点.