题目内容
14.已知f(x)为定义在区间(-∞,0)∪(0,+∞)上的偶函数,当x∈(0,+∞)时,f(x)=log2x.(1)求当x∈(-∞,0)时,函数f(x)的解析式.
(2)在给出的坐标系中画出函数f(x)的图象,写出函数f(x)的单调区间,并指出单调性.
分析 (1)设x∈(-∞,0),则-x∈(0,+∞),从而利用偶函数得f(x)=log2(-x)(x∈(-∞,0));
(2)分段作出函数图象,从而由图象知f(x)的单调增区间是:(0,+∞),单调减区间是:(-∞,0).
解答 解:(1)设x∈(-∞,0),则-x∈(0,+∞),
所以f(-x)=log2(-x),
又f(x)为定义在区间(-∞,0)∪(0,+∞)上的偶函数,
所以f(-x)=f(x),
所以f(x)=log2(-x)(x∈(-∞,0));
(2)作函数图象如下,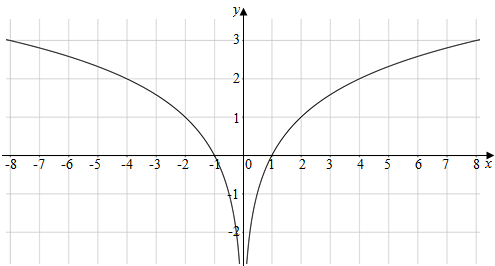
由图象可知,
f(x)的单调增区间是:(0,+∞),单调减区间是:(-∞,0).
点评 本题考查了函数的性质的应用及数形结合的思想应用,同时考查了学生的作图的能力.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
11.已知$\frac{π}{2}$≤β<α<$\frac{3π}{4}$,sin(α+β)=-$\frac{3}{5}$,cos(α-β)=$\frac{12}{13}$,则cos2β的值为( )
| A. | -$\frac{63}{65}$ | B. | $\frac{63}{65}$ | C. | $\frac{33}{65}$ | D. | -$\frac{33}{65}$ |
5.已知一次函数f(x)的图象不过第四象限,且f(f(x))=4x+3,则f(x)的表达式为( )
| A. | 2x+1 | B. | -2x-3 | C. | -2x+1 | D. | 2x+3 |
19.已知函数f(x)(x∈R)是奇函数,且当x>0时,f(x)=2x-1,则f(-1)=( )
| A. | 2 | B. | -2 | C. | -1 | D. | 1 |
4.已知$sinθ=\frac{4}{5}$,$cosθ=-\frac{3}{5}$,则θ是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |