题目内容
（1）已知x＞0，求x+
的最值；
（2）已知x＜0，求x+
的最值．
| 1 |
| x |
（2）已知x＜0，求x+
| 1 |
| x |
考点：基本不等式
专题：不等式的解法及应用
分析：利用基本不等式即可得出．
解答：
解：（1）当x＞0时，x+
≥2
=2，当且仅当x=1时取等号，
∴x+
的最小值为2，无最大值．
（2）∵x＜0，∴-x＞0，
∴x+
=-(-x+
)≤-2
=-2，当且仅当x=-1时取等号．
∴x+
的最大值为-2，无最小值．
| 1 |
| x |
x•
|
∴x+
| 1 |
| x |
（2）∵x＜0，∴-x＞0，
∴x+
| 1 |
| x |
| 1 |
| -x |
-x•
|
∴x+
| 1 |
| x |
点评：本题考查了基本不等式的性质，属于基础题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
如图所示，已知椭圆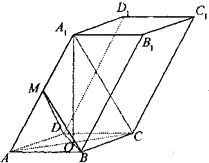
已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形，AC∩BD=O，AA1=2