题目内容
11. 如图,在底半径为5,高为10的圆锥中内接一个圆柱,
如图,在底半径为5,高为10的圆锥中内接一个圆柱,(1)写出圆柱的高h与圆柱的底面半径r的关系式
(2)当内接圆柱的底面半径为何值时,圆柱的表面积有最大值,最大值是多少?
分析 (1)设圆锥的高与圆柱的下底交点为M,与圆柱的上底交点为O,过O作圆锥底面的平行线OA,交圆锥于A,过M作OA的平行线MN,交圆锥于N,由题意△POA∽△PMN,由此能求出结果.
(2)圆柱的表面积S=πr2•h=πr2(10-2r)=10πr2-2πr3,0<r<5,由此利用导数性质能求出圆柱的表面积的最大值及相应的r的求法.
解答  解:(1)设圆锥的高与圆柱的下底交点为M,与圆柱的上底交点为O,过O作圆锥底面的平行线OA,交圆锥于A,
解:(1)设圆锥的高与圆柱的下底交点为M,与圆柱的上底交点为O,过O作圆锥底面的平行线OA,交圆锥于A,
过M作OA的平行线MN,交圆锥于N,
由题意△POA∽△PMN,
∴$\frac{10-h}{10}=\frac{r}{5}$,
整理,得h=10-2r.(0<r<5).
(2)圆柱的表面积S=πr2•h=πr2(10-2r)=10πr2-2πr3,0<r<5,
S′=20πr-6πr2,
由S′=0,得r=$\frac{10}{3}$,
当0<r<$\frac{10}{3}$时,S′>0;当$\frac{10}{3}<r<5$时,S′<0,
∴r=$\frac{10}{3}$时,圆柱的表面积有最大值,最大值为Smax=10π×$(\frac{10}{3})^{2}$-2$π(\frac{10}{3})^{3}$=$\frac{1000π}{27}$.
点评 本题考查圆柱的高与圆柱的底面半径的关系式的求法,考查当内接圆柱的底面半径为何值时,圆柱的表面积有最大值,最大值是多少的求法,是中档题,解题时要注意导数性质的合理运用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
7.已知点P(cosθ,sin2θ)和点Q(0,1)是两个相异点,则P、Q两点连线所在直线的倾斜角的取值范围为( )
| A. | [0,$\frac{π}{4}$] | B. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π) | C. | [-$\frac{π}{4}$,$\frac{π}{4}$] | D. | [$\frac{π}{4}$,$\frac{3π}{4}$] |
16.i是虚数单位,复数$\frac{(1+i)^{4}}{1-i}$的虚部为( )
| A. | 2i | B. | -2 | C. | i | D. | 1 |
20.设等差数列{an}满足a2=7,a4=3,Sn是数列{an}的前n项和,则使得Sn>0最大的自然数n是( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
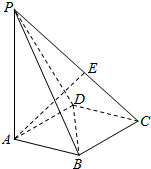 如图,底面为菱形P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AB.
如图,底面为菱形P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AB.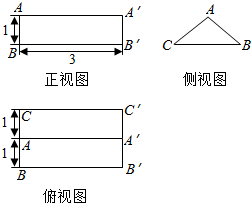 如图是一个几何体的三视图(单位:cm).
如图是一个几何体的三视图(单位:cm).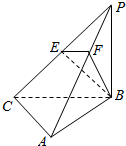 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.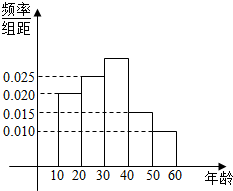 某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.
某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.