题目内容
16.i是虚数单位,复数$\frac{(1+i)^{4}}{1-i}$的虚部为( )| A. | 2i | B. | -2 | C. | i | D. | 1 |
分析 利用复数的运算法则即可得出.
解答 解:复数$\frac{(1+i)^{4}}{1-i}$=$\frac{-4}{1-i}$=$\frac{-4(1+i)}{(1-i)(1+i)}$=$\frac{-4(1+i)}{2}$=-2-2i的虚部为-2.
故选:B.
点评 本题考查了复数的运算法则,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
12.在区间(0,1)内任取一个数a,能使方程x2+2ax+$\frac{1}{2}$=0有两个不相等的实数根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{2-\sqrt{2}}{2}$ |
1.在复平面内,复数z=(a-1)+(a+1)i(a∈R,i为虚数单位)对应的点位于第三象限的充要条件是( )
| A. | a>1 | B. | a<1 | C. | a>-1 | D. | a<-1 |
8.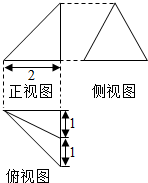 某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )
某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )
 某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )
某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )| A. | 5π | B. | $\frac{20}{3}π$ | C. | 8π | D. | $\frac{28}{3}π$ |
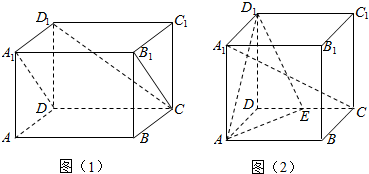
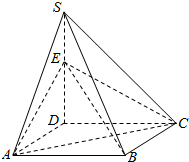 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=λa(0<λ≤1).
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=λa(0<λ≤1). 如图,在底半径为5,高为10的圆锥中内接一个圆柱,
如图,在底半径为5,高为10的圆锥中内接一个圆柱,



