题目内容
19.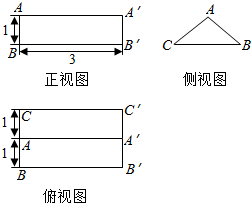 如图是一个几何体的三视图(单位:cm).
如图是一个几何体的三视图(单位:cm).(1)试写出该几何体的名称并画出该几何体的直观图(不要求写画法);
(2)求该几何体的表面积及体积.
分析 (1)几何体为平放的三棱柱,作出直观图;(2)根据三视图中数据的意义求出棱柱的底面边长和棱柱的高,代入公式计算即可.
解答 解:(1)三棱柱,直观图为:
(2)由三视图可知,该棱柱的高CC′=3,棱锥的底面ABC为等腰三角形,BC=2,三角形ABC的高为1,则腰AB=AC=$\sqrt{2}$,
∴表面积S=$\frac{1}{2}×2×1×2$+(2$+\sqrt{2}+\sqrt{2}$)×3=8+6$\sqrt{2}$(cm2),
三棱柱的三棱柱的体积V=$\frac{1}{2}×2×1×3$=3(cm3),
点评 本题考查了棱柱的三视图和直观图,棱柱的体积和表面积计算,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
14. 如图,已知正三棱锥P-ABC中,底面是正三角形,P在底面内的射影是正三角形的中心.若AB=1,侧面和底面所成的角是60°,则此棱锥的表面积是( )
如图,已知正三棱锥P-ABC中,底面是正三角形,P在底面内的射影是正三角形的中心.若AB=1,侧面和底面所成的角是60°,则此棱锥的表面积是( )
 如图,已知正三棱锥P-ABC中,底面是正三角形,P在底面内的射影是正三角形的中心.若AB=1,侧面和底面所成的角是60°,则此棱锥的表面积是( )
如图,已知正三棱锥P-ABC中,底面是正三角形,P在底面内的射影是正三角形的中心.若AB=1,侧面和底面所成的角是60°,则此棱锥的表面积是( )| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{5\sqrt{3}}{4}$ | C. | $\frac{1}{4}$+$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$+$\frac{\sqrt{3}}{4}$ |
8.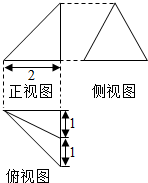 某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )
某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )
 某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )
某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )| A. | 5π | B. | $\frac{20}{3}π$ | C. | 8π | D. | $\frac{28}{3}π$ |
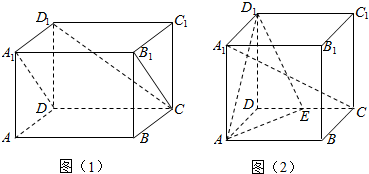
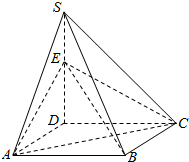 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=λa(0<λ≤1).
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=λa(0<λ≤1). 如图,在底半径为5,高为10的圆锥中内接一个圆柱,
如图,在底半径为5,高为10的圆锥中内接一个圆柱,