题目内容
3.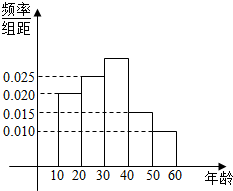 某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.
某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.(Ⅰ)求随机抽取的市民中年龄段在[30,40)的人数;
(Ⅱ)从不小于40岁的人中按年龄段分层抽样的方法随机抽取5人,求[50,60)年龄段抽取的人数;
(Ⅲ)从(Ⅱ)中方式得到的5人中再抽取2人作为本次活动的获奖者,求[50,60)年龄段仅1人获奖的概率.
分析 (I)由频率分布直方图求出随机抽取的市民中年龄段在[30,40)的频率,由此能求出随机抽取的市民中年龄段在[30,40)的人数.
(II)由频率分布直方图求出不小于40岁的人的频数是25人,由此能求出在[50,60)年龄段抽取的人数.
(III)所抽5人中有3人是在[40,50)年龄段,有2人是在[50,60)年龄段,由此利用列举法能求出从5人中再抽取2人作为本次活动的获奖者,[50,60)年龄段仅1人获奖的概率.
解答 解:(I)由频率分布直方图知,随机抽取的市民中年龄段在[30,40)的频率为:
1-10×(0.020+0.025+0.015+0.010)=0.3,
∴随机抽取的市民中年龄段在[30,40)的人数为100×0.3=30人. …(3分)
(II)由(I)知,年龄段在[40,50),[50,60)的人数分别为100×0.15=15人,
100×0.1=10人,即不小于40岁的人的频数是25人,
∴在[50,60)年龄段抽取的人数为10×$\frac{5}{25}$=2人. …(6分)
(III)由(II)知,所抽5人中有3人是在[40,50)年龄段中取得,记为A1,A2,A3;
有2人是在[50,60)年龄段中取得,记为B1,B2,
∴从5人中再抽取2人作为本次活动的获奖者的可能有(A1,A2),(A1,A3),(A1,B1),
(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2)共10种,
其中[50,60)年龄段仅1人获奖的情况有 (A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2)共 6种,
∴[50,60)年龄段仅1人获奖的概率为P=$\frac{6}{10}=\frac{3}{5}$. …(12分)
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

 如图,已知正三棱锥P-ABC中,底面是正三角形,P在底面内的射影是正三角形的中心.若AB=1,侧面和底面所成的角是60°,则此棱锥的表面积是( )
如图,已知正三棱锥P-ABC中,底面是正三角形,P在底面内的射影是正三角形的中心.若AB=1,侧面和底面所成的角是60°,则此棱锥的表面积是( )| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{5\sqrt{3}}{4}$ | C. | $\frac{1}{4}$+$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$+$\frac{\sqrt{3}}{4}$ |
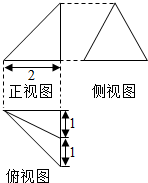 某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )
某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )| A. | 5π | B. | $\frac{20}{3}π$ | C. | 8π | D. | $\frac{28}{3}π$ |
| A. | 24 | B. | 48 | C. | 72 | D. | 120 |
 如图,在底半径为5,高为10的圆锥中内接一个圆柱,
如图,在底半径为5,高为10的圆锥中内接一个圆柱,