题目内容
20.设等差数列{an}满足a2=7,a4=3,Sn是数列{an}的前n项和,则使得Sn>0最大的自然数n是( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 利用等差数列的通项公式可得:an=-2n+11,可见{an}是减数列,且a5>0>a6,a5+a6=0,再利用前n项和公式即可得出.
解答 解:设等差数列{an}公差为d,∵a2=7,a4=3,
∴$\left\{\begin{array}{l}{{a}_{1}+d=7}\\{{a}_{1}+3d=3}\end{array}\right.$,解得d=-2,a1=9.
∴an=9-2(n-1)=-2n+11,
∴数列{an}是减数列,且a5>0>a6,a5+a6=0,
于是${S_9}=\frac{{2{a_5}}}{2}•9>0$,${S_{10}}=\frac{{{a_5}+{a_6}}}{2}•10=0$,${S_{11}}=\frac{{2{a_6}}}{2}•11<0$,
故选:A.
点评 本题考查了等差数列的通项公式及其前n项和公式、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
8.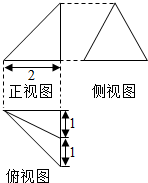 某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )
某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )
 某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )
某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )| A. | 5π | B. | $\frac{20}{3}π$ | C. | 8π | D. | $\frac{28}{3}π$ |
 如图,在底半径为5,高为10的圆锥中内接一个圆柱,
如图,在底半径为5,高为10的圆锥中内接一个圆柱,




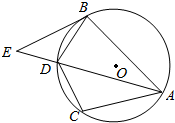 如图,A,B,C,D是半径为1的⊙O上的点,BD=DC=1,⊙O在点B处的切线交AD的延长线于点E.
如图,A,B,C,D是半径为1的⊙O上的点,BD=DC=1,⊙O在点B处的切线交AD的延长线于点E.