Question

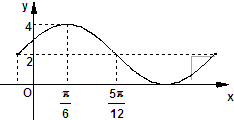已知函数f（x）=Asin（ωx+ϕ）+B的一部分图象如图所示，如果A＞0，ω＞0，|φ|＜

π

2

，
（1）求函数f（x）的解析式．
（2）记g（x）=log₂[f（x）-1]，求函数g（x）的定义域．
（3）若对任意的x∈[-

π

6

，

π

6

]，不等式log

1

2

f（x）＞m-3恒成立，求实数m的取值范围．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,对数函数的图像与性质

专题：三角函数的图像与性质

分析：（1）直接由函数图象得到A和T，利用走起公式求ω，再由三角函数的对称性得到φ的等式，借助于φ的范围求φ；
（2）直接由g（x）=log₂[f（x）-1]的真数大于0解三角不等式求得函数g（x）的定义域；
（3）由x的范围求得f（x）的范围，结合对数函数的单调性得到关于m的不等式，求解不等式得答案．

解答： 解：（1）由图象可知A=

4-0

2

=2，B=

4+0

2

=2，

T

4

=

5π

12

-

π

6

=

π

4

，
∴T=π，
∴ω=

2π

T

=2，
∴2×

π

6

+ϕ=2kπ+

π

2

，ϕ=2kπ+

π

6

(k∈Z)，
∵|ϕ|＜

π

2

，
∴ϕ=

π

6

；
（2）由（1）知f(x)=2sin(2x+

π

6

)+2，要使函数g（x）=log₂[f（x）-1]有意义，
有f（x）-1＞0，故2sin(2x+

π

6

)+1＞0，即sin(2x+

π

6

)＞-

1

2

，
∴2kπ-

π

6

＜2x+

π

6

＜2kπ+

7π

6

，
解得kπ-

π

6

＜x＜kπ+

π

2

(k∈Z)．
∴函数g（x）的定义域为{x|2kπ-

π

6

＜2x+

π

6

＜2kπ+

7π

6

，k∈Z}；
（3）对?x∈[-

π

6

，

π

6

]，有-

π

6

＜2x+

π

6

＜

π

2

，
∴-

1

2

≤sin(2x+

π

6

)≤1，
∴1≤f（x）≤4．
则log

1

2

4≤log

1

2

f(x)≤log

1

2

1，即-2≤log

1

2

f(x)≤0．
若log

1

2

f(x)＞m-3对?x∈[-

π

6

，

π

6

]恒成立，
即log

1

2

f(x)的最小值大于m-3．
故-2＞m-3，即m＜1．

点评：本题考查了由y=Asin（ωx+φ）的部分图象求函数解析式，考查了与三角函数有关的复合函数的定义域的求法，考查了三角函数的值域，体现了数学转化思想方法，是中档题．