题目内容
16.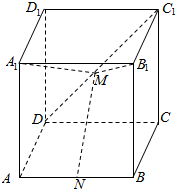 如图所示,在长方体ABCD-A1B1C1D1中,AD=1,AB=AA1=2,N、M分别是AB、C1D的中点.
如图所示,在长方体ABCD-A1B1C1D1中,AD=1,AB=AA1=2,N、M分别是AB、C1D的中点.(1)求证:NM∥平面A1ADD1;
(2)求证:NM⊥平面A1B1M.
分析 (1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能证明MN∥平面A1ADD1.
(2)由$\overrightarrow{MN}•\overrightarrow{{A}_{1}{B}_{1}}$=0,$\overrightarrow{MN}•\overrightarrow{{A}_{1}M}$=0,利用向量法能证明NM⊥平面A1B1M.
解答 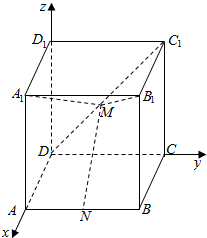 证明:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
证明:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
∵在长方体ABCD-A1B1C1D1中,AD=1,AB=AA1=2,N、M分别是AB、C1D的中点,
∴M(0,1,1),N(1,1,0),$\overrightarrow{MN}$=(1,0,-1),
∵平面A1ADD1的法向量$\overrightarrow{n}$=(0,1,0),
∴$\overrightarrow{MN}•\overrightarrow{n}$=0,
∵MN?平面A1ADD1,∴MN∥平面A1ADD1.
(2)A1(1,0,2),B1(1,2,2),$\overrightarrow{{A}_{1}{B}_{1}}$=(0,2,0),$\overrightarrow{{A}_{1}M}$=(-1,1,-1),
∴$\overrightarrow{MN}•\overrightarrow{{A}_{1}{B}_{1}}$=0,$\overrightarrow{MN}•\overrightarrow{{A}_{1}M}$=0,
∴MN⊥A1B1,MN⊥A1M,
∵A1B1∩A1M=A1,
∴NM⊥平面A1B1M.
点评 本题考查线面平行、线面垂直的证明,是基础题,解题时要认真审题,注意向量法的合理运用.

| A. | (2,3] | B. | [2,3] | C. | (2,3) | D. | (-∞,3] |
| A. | 3$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\sqrt{34}$ | D. | 5$\sqrt{2}$ |
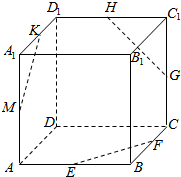 已知正方体ABCD-A1B1C1D1中,点E,F,G,H,K,M分别棱AB,BC,CC1,C1D1,A1D1,A1A的中点,如图,求证:EF,GH,KM共面.
已知正方体ABCD-A1B1C1D1中,点E,F,G,H,K,M分别棱AB,BC,CC1,C1D1,A1D1,A1A的中点,如图,求证:EF,GH,KM共面.