题目内容
18.一个正方体的棱长为2cm,它的顶点都在一个球面上,则球的半径是( )cm.| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 利用正方体的对角线的长度等于球的直径,求解即可.
解答 解:一个正方体的棱长为2cm,它的顶点都在一个球面上,
则球的半径是:$\frac{1}{2}$×$2\sqrt{3}$=$\sqrt{3}$.
故选:C.
点评 本题考查球的内接体,球的半径的求法,是基础题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
3.两平行线3x-4y-12=0与6x+ay+16=0间的距离是( )
| A. | $\frac{28}{5}$ | B. | 4 | C. | $\frac{14}{5}$ | D. | $\frac{4}{5}$ |
7.已知$p:\frac{1}{x-2}≥1$,q:|x-a|<1.若q是p的必要不充分条件,则实数a的取值范围是( )
| A. | (2,3] | B. | [2,3] | C. | (2,3) | D. | (-∞,3] |
8.在长方体ABCD-A1B1C1D1中,AB=6,BC=4,AA1=2,P,Q分别为棱AA1,C1D1的中点,则从点P出发,沿长方体表面到达点Q的最短路径的长度为( )
| A. | 3$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\sqrt{34}$ | D. | 5$\sqrt{2}$ |
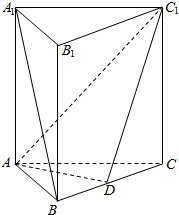 如图.在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D.
如图.在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D.
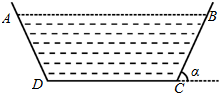 2015年春,某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<$\frac{π}{2}$)为多大时,水渠中水的流失量最小?
2015年春,某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<$\frac{π}{2}$)为多大时,水渠中水的流失量最小?