题目内容
若函数y=f(x)的图象与函数y=ax(a>0且a≠1)的图象关于直线y=x对称,且f(3)=1,则f(x)=( )
| A、log3x | ||
B、(
| ||
C、log
| ||
| D、3x |
考点:反函数
专题:函数的性质及应用
分析:由题意可知函数y=f(x)与函数y=ax(a>0且a≠1)互为反函数,求出y=ax的反函数,再由f(3)=1求出a值得答案.
解答:
解:∵函数y=f(x)的图象与函数y=ax(a>0且a≠1)的图象关于直线y=x对称,
∴函数y=f(x)与函数y=ax(a>0且a≠1)互为反函数,
由y=ax(a>0且a≠1),得x=logay,
则f(x)=logax,
由f(3)=1,得loga3=1,a=3.
∴f(x)=log3x.
故选:A.
∴函数y=f(x)与函数y=ax(a>0且a≠1)互为反函数,
由y=ax(a>0且a≠1),得x=logay,
则f(x)=logax,
由f(3)=1,得loga3=1,a=3.
∴f(x)=log3x.
故选:A.
点评:本题考查了反函数的求法,考查了互为反函数的两个函数图象间的关系,是基础题.

练习册系列答案
相关题目
如图是函数f(x)=Asin(ωx+φ)的部分图象,则f(x)的表达式为( )
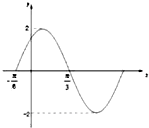

A、f(x)=2sin(2x-
| ||
B、f(x)=2sin(2x+
| ||
C、f(x)=2sin(x+
| ||
D、f(x)=2sin(2x-
|
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.若极坐标方程为ρcosθ=4的直线与曲线
(t为参数)相交于A,B两点,则|AB|=( )
|
| A、2 | B、4 | C、8 | D、16 |
当y=f(x)是下列的( )时,f′(x)一定是增函数.
| A、二次函数 | B、反比例函数 |
| C、对数函数 | D、指数函数 |
已知a,b为实数,则“a+b≥2”是“a≥1且b≥1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知全集U=R,集合A={x|x<3},B={x|lnx<0},则A∩∁UB( )
| A、{x|1<x<3} |
| B、{x|x≤0或1≤x<3} |
| C、{x|x<3} |
| D、{x|1≤x<3} |