题目内容
已知数列{an},a1=1且an-1-an=an-1an(n≥2,n∈N*),则Tn=a1a2+a2a3+…+anan-1的值为 .
考点:数列的求和
专题:等差数列与等比数列
分析:a1=1且an-1-an=an-1an,可得
-
=1,数列{
}成等差数列,利用等差数列的通项公式及“裂项求和”即可得出.
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| an |
解答:
解:∵a1=1且an-1-an=an-1an,
∴
-
=1,
∴数列{
}成等差数列,
∴
=1+(n-1)×1=n,
∴an=
.
∴Tn=a1a2+a2a3+…+anan-1=(a1-a2)+(a2-a3)+…+(an-1-an)
=a1-an
=1-
.
=
.
故答案为:
.
∴
| 1 |
| an |
| 1 |
| an-1 |
∴数列{
| 1 |
| an |
∴
| 1 |
| an |
∴an=
| 1 |
| n |
∴Tn=a1a2+a2a3+…+anan-1=(a1-a2)+(a2-a3)+…+(an-1-an)
=a1-an
=1-
| 1 |
| n |
=
| n-1 |
| n |
故答案为:
| n-1 |
| n |
点评:本题考查了等差数列的通项公式及“裂项求和”,考查了变形能力与计算能力,属于中档题.

练习册系列答案
相关题目
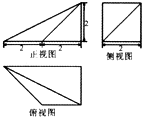
某几何体的三视图如图所示,则这个几何体的体积为( )

A、
| ||
B、
| ||
| C、8 | ||
| D、4 |
抛物线 x2=y的准线方程是( )
| A、4x+1=0 |
| B、4y+1=0 |
| C、2x+1=0 |
| D、2y+1=0 |