题目内容
设函数f(x)=loga(1+ax)-loga(1-ax),其中a>0,且a≠1,
(1)当a=2时,解不等式f(x)-1>0;
(2)当a>1时,若关于x的不等式f(x)≥log
(a>1)恒成立,求a的取值范围;
(3)若f(x0)=x0-1,证明|x0|<1.
(1)当a=2时,解不等式f(x)-1>0;
(2)当a>1时,若关于x的不等式f(x)≥log
(8x) a |
(3)若f(x0)=x0-1,证明|x0|<1.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)log2(1+2x)-log2(1-2x)>1,转化为:
求解即可.
(2)loga(1+ax)-loga(1-ax)>log
(a>1),
即
即对任意的x∈[0,
],8ax2+(a-8)x+1>0,
8ax+
+(a-2)>0.转化为最值求解判断
(3)loga(1+ax0)-loga(1-ax0)=x0-1,即
=a x0-1,构造函数,运用单调性证明.
|
(2)loga(1+ax)-loga(1-ax)>log
(8x) a |
|
|
即对任意的x∈[0,
| 1 |
| a |
8ax+
| 1 |
| x |
(3)loga(1+ax0)-loga(1-ax0)=x0-1,即
| 1+ax0 |
| 1-ax0 |
解答:
解;(1)当a=2时,f(x)=log2(1+2x)-log2(1-2x),由f(x)-1>0得:
log2(1+2x)-log2(1-2x)>1,
转化为:
,
解不等式组得:
<x<
;
故:解不等式f(x)-1>0为(
,
).
(2)由f(x)≥log
(a>1)
loga(1+ax)-loga(1-ax)>log
(a>1),
即
即对任意的x∈[0,
],8ax2+(a-8)x+1>0,
8ax+
+(a-2)>0.
g(x)=8ax+
+(a-2)>0的图象在x轴上方,
g(x)min>0,即
或
,
解不等式得a≥8或
,
即a的范围为:a>1;
(3)∵f(x0)=x0-1,函数f(x)=loga(1+ax)-loga(1-ax),
loga(1+ax0)-loga(1-ax0)=x0-1,
即
=a x0-1,
即-1-
=a x0-1,
构造函数,根据单调性可判断-1<x0<1,
不等式|x0|<1成立.
log2(1+2x)-log2(1-2x)>1,
转化为:
|
解不等式组得:
| 1 |
| 6 |
| 1 |
| 2 |
故:解不等式f(x)-1>0为(
| 1 |
| 6 |
| 1 |
| 2 |
(2)由f(x)≥log
(8x) a |
loga(1+ax)-loga(1-ax)>log
(8x) a |
|
|
即对任意的x∈[0,
| 1 |
| a |
8ax+
| 1 |
| x |
g(x)=8ax+
| 1 |
| x |
g(x)min>0,即
|
|
解不等式得a≥8或
|
即a的范围为:a>1;
(3)∵f(x0)=x0-1,函数f(x)=loga(1+ax)-loga(1-ax),
loga(1+ax0)-loga(1-ax0)=x0-1,
即
| 1+ax0 |
| 1-ax0 |
即-1-
| 2 |
| ax0-1 |
构造函数,根据单调性可判断-1<x0<1,
不等式|x0|<1成立.
点评:本题综合考查了函数的性质,运用解决复杂的求解范围问题,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设定义在(1,e)上函数f(x)=
(a∈R).若曲线y=1+cosx上存在点(x0,y0)使得f(f(y0))=y0,则实数a的取值范围是( )
| x-lnx+a |
| A、[-1,2+ln2] |
| B、(0,2+ln2] |
| C、[-1,e2-e+1) |
| D、(0,e2-e+1) |
设集合M={x|0≤x≤2},N={y|0≤y≤2},给出下列4个图形,其中能表示集合M到N的函数关系的有( )
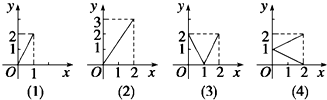

| A、0个 | B、1个 | C、2个 | D、3个 |