题目内容

从0，1，2，3，4中任取3个不同的数分别记作抛物线y=ax2+bx+c，其中顶点在y轴上的抛物线共有
 
条．
考点：二次函数的性质
专题：函数的性质及应用
分析：通过组合结合二次函数的性质，从而得出答案．
解答： 解：a不能取0，共有
C
1
4
种取法，
顶点在y轴上，b只能为0，
c共有
C
1
5
种取法，
∴有
C
1
4
C
1
5
=20，
故答案为：20．
点评：本题考查了二次函数的性质，排列组合问题，是一道基础题．
练习册系列答案
相关题目
已知数列{an}的通项公式an=
1
n(n+1)
，sn是它的前n项和，则s2014=
 
．
在平面直角坐标系xOy中，已知点A（-6，0），B（4，0），C（9，m），△ABC的外接圆为⊙M．
（1）若∠CAB=30°，求m值；
（2）若⊙M与直线l：ax+2y+6=0相切于点A，求⊙M的方程；
（3）若⊙M与y轴交于P、Q两点，求PQ长的最小值．
已知椭圆的两个焦点坐标分别是（-
2
，0），（
2
，0），并且经过点（
2
2
，
30
6
）．
（1）求椭圆的标准方程；
（2）若斜率为k的直线l经过点（0，-2），且与椭圆交于不同的两点A、B，求△OAB面积的最大值．
已知a，b是正数，a+b=1，求（a+
1
a
）+（b+
1
b
）的最小值．
若a，b是任意非零的常数，对于函数y=f（x）有以下5个命题：
①f（x）是T=2a的周期函数的充要条件是f（x+a）=f（x-a）；
②f（x）是T=2a的周期函数的充要条件是f（x+a）=-f（x）；
③若f（x）关于直线x=
a
2
对称，且f（x+a）=-f（x），则f（x）是奇函数；
④若f（x）是奇函数且是T=2a的周期函数，则f（x）的图形关于直线x=
a
2
 对称；
⑤若f（x）关于点（a，0）对称，关于直线x=b对称，则f（x）是T=4（a-b）的周期函数．
其中正确命题的序号为
 
．
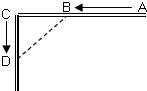如图，快艇和轮船分别从A地和C地同时开出，航行路线互相垂直，快艇的速度为40千米/时，轮船的速度是15千米/时，A、C两地间的距离是120千米．问经过多少时间．快艇和轮船之间的距离最小？（精确到0.1小时）
若函数f（x）=
1
3
x3+x2+mx是R上的单调函数，则实数m的取值范围是（　　）
A、（1，+∞）
B、（-∞，1）
C、[1，+∞）
D、（-∞，1]
若实数x，y满足不等式组
y≤5
2x+y+3≥0
y-x-1≥0
，则z=|x|+2y的最大值是（　　）
A、10B、11C、13D、14

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网