题目内容
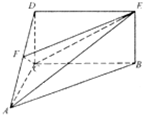 如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=
如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=| 1 |
| 2 |
(1)求证:AB∥平面CEF;
(2)求几何体ABCDE被平面CEF分成的上下两部分的体积之比.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:计算题,证明题,空间位置关系与距离
分析:(1)连结BD,交CE于点H,连结FH,从而FH是△ABD的中位线,从而证明AB∥平面CEF;
(2)由题意知,点F到平面BCDE的距离是点A到平面BCDE的距离的一半,S△CDE=
S矩形BCDE,从而得VF-CDE:VA-BCDE=1:4,从而得到几何体ABCDE被平面CEF分成的上下两部分的体积之比为1:3.
(2)由题意知,点F到平面BCDE的距离是点A到平面BCDE的距离的一半,S△CDE=
| 1 |
| 2 |
解答:
 解:(1)证明:如图,连结BD,交CE于点H,连结FH,
解:(1)证明:如图,连结BD,交CE于点H,连结FH,
∵四边形BCDE为矩形,
∴H是线段BD的中点,
又∵点F是线段AD的中点,
∴FH是△ABD的中位线,
∴FH∥AB,
又∵FH?平面CEF,AB?平面CEF;
∴AB∥平面CEF;
(2)∵点F是线段AD的中点.
∴点F到平面BCDE的距离是点A到平面BCDE的距离的一半,
又∵S△CDE=
S矩形BCDE,
∴VF-CDE:VA-BCDE=1:4,
∴几何体ABCDE被平面CEF分成的上下两部分的体积之比为1:3.
 解:(1)证明:如图,连结BD,交CE于点H,连结FH,
解:(1)证明:如图,连结BD,交CE于点H,连结FH,∵四边形BCDE为矩形,
∴H是线段BD的中点,
又∵点F是线段AD的中点,
∴FH是△ABD的中位线,
∴FH∥AB,
又∵FH?平面CEF,AB?平面CEF;
∴AB∥平面CEF;
(2)∵点F是线段AD的中点.
∴点F到平面BCDE的距离是点A到平面BCDE的距离的一半,
又∵S△CDE=
| 1 |
| 2 |
∴VF-CDE:VA-BCDE=1:4,
∴几何体ABCDE被平面CEF分成的上下两部分的体积之比为1:3.
点评:本题考查了学生的空间想象力,同时考查了作图能力及线面平行的判断、几何体的体积求法等,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)=
x3+x2+mx是R上的单调函数,则实数m的取值范围是( )
| 1 |
| 3 |
| A、(1,+∞) |
| B、(-∞,1) |
| C、[1,+∞) |
| D、(-∞,1] |
若直线a平行于平面α,则下列结论错误的是( )
| A、a平行于α内的所有直线 |
| B、α内有无数条直线与a平行 |
| C、直线a上的点到平面α的距离相等 |
| D、α内存在无数条直线与a成90°角 |
若实数x,y满足不等式组
,则z=|x|+2y的最大值是( )
|
| A、10 | B、11 | C、13 | D、14 |