题目内容
已知向量
(x,y),
(a,b),
和
均为单位向量,试证明:ax+by≤1.
| m |
| n |
| m |
| n |
考点:平面向量数量积的性质及其运算律
专题:平面向量及应用
分析:根据向量的数量积的定义以及向量的数量积的坐标运算结合余弦的有界性解答.
解答:
解:因为向量
(x,y),
(a,b),
和
均为单位向量,
所以
•
=ax+by=|
||
|cos<
,
>=cos<
,
>≤1;
故结论成立.
| m |
| n |
| m |
| n |
所以
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
故结论成立.
点评:本题考查了向量的数量积的定义以及坐标运算属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)=
x3+x2+mx是R上的单调函数,则实数m的取值范围是( )
| 1 |
| 3 |
| A、(1,+∞) |
| B、(-∞,1) |
| C、[1,+∞) |
| D、(-∞,1] |
若直线a平行于平面α,则下列结论错误的是( )
| A、a平行于α内的所有直线 |
| B、α内有无数条直线与a平行 |
| C、直线a上的点到平面α的距离相等 |
| D、α内存在无数条直线与a成90°角 |
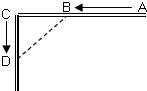 如图,快艇和轮船分别从A地和C地同时开出,航行路线互相垂直,快艇的速度为40千米/时,轮船的速度是15千米/时,A、C两地间的距离是120千米.问经过多少时间.快艇和轮船之间的距离最小?(精确到0.1小时)
如图,快艇和轮船分别从A地和C地同时开出,航行路线互相垂直,快艇的速度为40千米/时,轮船的速度是15千米/时,A、C两地间的距离是120千米.问经过多少时间.快艇和轮船之间的距离最小?(精确到0.1小时)