题目内容
14．圆锥底面半径为10，母线长为30，从底面圆周上一点，绕侧面一周再回到该点的最短路线的长度是30$\sqrt{3}$．分析 作出侧面展开图，则扇形的弦长为最短距离．
解答 
解：圆锥的侧面展开图为半径为30，弧长为20π的扇形AOB，
∴最短距离为AB的长．
扇形的圆心角为$\frac{20π}{30}$=$\frac{2π}{3}$，
∴AB=$\sqrt{3{0}^{2}+3{0}^{2}-2×30×30×cos\frac{2π}{3}}$=30$\sqrt{3}$．
故答案为：30$\sqrt{3}$．
点评 本题考查了圆锥的结构特征，最短距离求解，将曲面转化为平面是解题关键，属于中档题．
练习册系列答案
英才计划期末调研系列答案
精英口算卡系列答案
相关题目
8．我国古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮，有人送来米1534石，验得米内夹谷，抽样取米一把，数得254粒肉夹谷56粒，则这批米内夹谷约为（ ）
| A． | 1365石 | B． | 338 石 | C． | 168石 | D． | 134石 |
2．已知$\sqrt{2+\frac{2}{3}}=2\sqrt{\frac{2}{3}}$，$\sqrt{3+\frac{3}{8}}=3\sqrt{\frac{3}{8}}$，$\sqrt{4+\frac{4}{15}}=4\sqrt{\frac{4}{15}}$，…，$\sqrt{m+\frac{m}{t}}=m\sqrt{\frac{m}{t}}$（m，t∈N*且m≥2），若不等式λm-t-3＜0恒成立，则实数λ的取值范围为（ ）
| A． | $[2\sqrt{2}，+∞）$ | B． | $（-∞，2\sqrt{2}）$ | C． | （-∞，3） | D． | [1，3] |
6．在区间[1，5]和[2，4]上分别各取一个数，记为m和n，则方程$\frac{x^2}{m^2}+\frac{y^2}{n^2}=1$表示焦点在x轴上的椭圆的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
3．运行如图所示的程序框图，输出的S值等于$\frac{{{2^{10}}-1}}{{{2^{10}}}}$，则判断框内可以填（ ）
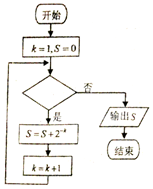
| A． | k≤8？ | B． | k≤9？ | C． | k≤10？ | D． | k≤11？ |