题目内容
3.运行如图所示的程序框图,输出的S值等于$\frac{{{2^{10}}-1}}{{{2^{10}}}}$,则判断框内可以填( )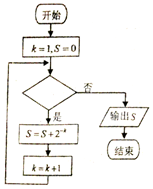
| A. | k≤8? | B. | k≤9? | C. | k≤10? | D. | k≤11? |
分析 模拟执行程序框图,依次写出每次循环得到的S,k的值,当k=11时,由题意,此时满足条件,退出循环,输出S的值为,则可得判断框中应该填的条件.
解答 解:模拟程序的运行,可得
s=0,k=1
满足条件,执行循环体,s=$\frac{1}{2}$,k=2
满足条件,执行循环体,s=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$,k=3
…
满足条件,执行循环体,s=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{k}}$=$\frac{1}{2}×$$\frac{1-(\frac{1}{2})^{k}}{1-\frac{1}{2}}$=1-($\frac{1}{2}$)k=$\frac{{2}^{k}-1}{{2}^{k}}$,k=k+1
由题意,此时k=10+1=11,应该不满足条件,退出循环,输出s的值为$\frac{{{2^{10}}-1}}{{{2^{10}}}}$,
则判断框内可以填k≤10?.
故选:C.
点评 本题主要考查程序框图的识别和运行,根据条件进行模拟运算是解决本题的关键,属于基础题.

练习册系列答案
相关题目
11.在三棱锥ABCD各边AB、BC、CD、DA上分别取E、F、G、H四点,如果EF、GH相交于点P,那么( )
| A. | 点P必在直线AC上 | B. | 点P必在直线BD上 | ||
| C. | 点P必在平面DBC内 | D. | 点P必在平面ABC外 |
15.《数书九章》是中国南宋时期杰出数学家秦九韶的著作,全书十八卷共八十一个问题,分为九类,每类九个问题,《数书九章》中记录了秦九昭的许多创造性成就,其中在卷五“三斜求职”中提出了已知三角形三边a,b,c求面积的公式,这与古希腊的海伦公式完成等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积.”若把以上这段文字写成公式,即S=$\sqrt{\frac{1}{4}[{c^2}{a^2}-{{(\frac{{{c^2}+{a^2}-{b^2}}}{2})}^2}]}$,现有周长为10+2$\sqrt{7}$的△ABC满足sinA:sinB:sinC=2:3:$\sqrt{7}$,则用以上给出的公式求得△ABC的面积为( )
| A. | $6\sqrt{3}$ | B. | $4\sqrt{7}$ | C. | $8\sqrt{7}$ | D. | 12 |
12.某车间需要确定加工零件的加工时间,进行了若干次试验.根据收集到的数据(如表):
由最小二乘法求得回归直线方程$\hat y=0.67x+\hat a$,则$\hat a$的值为54.9.
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 68 | 75 | 81 | 89 |