题目内容
在极坐标系中,直线l1的极坐标方程为ρ(2cosθ+sinθ)=2,直线l2的参数方程为
(t为参数),若直线l1与直线l2平行,则k的值为 .
|
考点:简单曲线的极坐标方程
专题:直线与圆
分析:首先把极坐标方程转化为直角坐标方程2x+y-2=0,再把参数方程转化为直角坐标方程kx+2y-4-k=0,进一步利用直线平行的充要条件求的结果.
解答:
解:在极坐标系中,直线l1的极坐标方程为ρ(2cosθ+sinθ)=2转化为直角坐标方程为:2x+y-2=0
直线l2的参数方程为
(t为参数)转化为直角坐标:方程为:kx+2y-4-k=0
由于若直线l1与直线l2平行
则:
=
解得:k=4
故答案为:4
直线l2的参数方程为
|
由于若直线l1与直线l2平行
则:
| k |
| 2 |
| 2 |
| 1 |
故答案为:4
点评:本题考查的知识要点:极坐标方程和直角坐标方程的互化,参数方程和直角坐标方程的互化,直线平行的充要条件及相关的运算问题.

练习册系列答案
相关题目
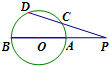 如图所示,AB是半径等于3的⊙O的直径,CD是⊙O的弦,BA,DC的延长线交于点P,若PA=4,PC=5,则DC=
如图所示,AB是半径等于3的⊙O的直径,CD是⊙O的弦,BA,DC的延长线交于点P,若PA=4,PC=5,则DC=