题目内容
cos(15°-θ)+cos(θ+45°)-
sin(75°-θ)的值为 .
| 3 |
考点:两角和与差的正弦函数,两角和与差的余弦函数
专题:计算题,三角函数的求值
分析:将75°-θ换为60°+15°-θ,由两角和的正弦公式展开,化简整理,再由两角差的余弦公式,注意逆用,即可得到结果.
解答:
解:cos(15°-θ)+cos(θ+45°)-
sin(75°-θ)
=cos(15°-θ)+cos(θ+45°)-
sin(60°+15°-θ)
=cos(15°-θ)-
(
cos(15°-θ)+
sin(15°-θ))+cos(θ+45°)
=-
cos(15°-θ)-
sin(15°-θ)+cos(θ+45°)
=-cos(60°-15°+θ)+cos(θ+45°)
=0.
故答案为:0.
| 3 |
=cos(15°-θ)+cos(θ+45°)-
| 3 |
=cos(15°-θ)-
| 3 |
| ||
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| ||
| 2 |
=-cos(60°-15°+θ)+cos(θ+45°)
=0.
故答案为:0.
点评:本题考查两角和的正弦和两角差的余弦公式的运用,注意角的变换,考查化简和整理,以及逆用公式的能力,属于中档题.

练习册系列答案
相关题目
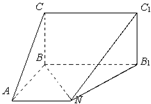 如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形,
如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形,且AB⊥BB1,BC=AB=AN=
| 1 |
| 2 |
(1)求证:BN⊥平面C1B1N;
(2)求此五面体的体积.
设F1,F2是椭圆
+
=1的两个焦点,点M在椭圆上,若△MF1F2是直角三角形,则△MF1F2的面积等于( )
| x2 |
| 25 |
| y2 |
| 16 |
A、
| ||
B、
| ||
| C、16 | ||
D、
|
已知坐标满足方程F(x,y)=0的点都在曲线C上,那么( )
| A、曲线C上的点的坐标都适合方程F(x,y)=0 |
| B、凡坐标不适合F(x,y)=0的点都不在C上 |
| C、不在C上的点的坐标不必适合F(x,y)=0 |
| D、不在C上的点的坐标有些适合F(x,y)=0,有些不适合F(x,y)=0 |