题目内容
已知幂函数f（x）=（m2-m-1）xm2-2m-3，且当x＞0时，y是减函数，则m的值为 ．
考点：幂函数的性质
专题：函数的性质及应用
分析：根据幂函数的系数一定为1可先确定参数m的值，再根据单调性进行排除，可得答案．
解答：
解：∵函数f（x）=（m2-m-1）xm2-2m-3为幂函数，
∴m2-m-1=1，
解得：m=-1或m=2．
当m=-1时，函数为y=x0在x＞0时不是减函数，不满足题意，
当m=2时，函数为y=x-3在x＞0时是减函数，满足题意，
故m=2，
故答案为：2
∴m2-m-1=1，
解得：m=-1或m=2．
当m=-1时，函数为y=x0在x＞0时不是减函数，不满足题意，
当m=2时，函数为y=x-3在x＞0时是减函数，满足题意，
故m=2，
故答案为：2
点评：本题主要考查幂函数的表达形式以及幂函数的单调性，属于基础题．
练习册系列答案
小学教材完全解读系列答案
相关题目
函数f（x）的图象如图所示，下列数值排序正确的是（ ）
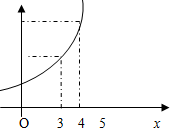
| A、0＜f′（3）＜f′（4）＜f（4）-f（3） |
| B、0＜f′（3）＜f（4）-f（3）＜f′（4） |
| C、0＜f′（4）＜f′（3）＜f（4）-f（3） |
| D、0＜f（4）-f（3）＜f′（3）＜f′（4） |
设函数y=f（x），x∈[a，b]，其导函数的图象如图所示，则函数y=f（x）的减区间是（ ）
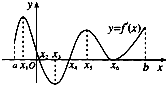
| A、（x1，x3） |
| B、（x2，x4） |
| C、（x4，x6） |
| D、（x5，x6） |