题目内容
已知奇函数f(x),偶函数g(x)满足f(x)+g(x)=ax(a>0,a≠1),求f(x)和g(x)的解析式.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:利用函数的奇偶性定义,列方程组求解解析式,即可完成答案.
解答:
解:∵奇函数f(x),偶函数g(x)∴f(-x)=-f(x),g(-x)=g(x)
由∵f(x)+g(x)=ax∴f(-x)+g(-x)=-ax,即-f(x)+g(x)=-ax,
联合求解得:g(x)=0,f(x)=ax
由∵f(x)+g(x)=ax∴f(-x)+g(-x)=-ax,即-f(x)+g(x)=-ax,
联合求解得:g(x)=0,f(x)=ax
点评:本题考查了奇偶函数的定义再求函数解析式中的应用,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
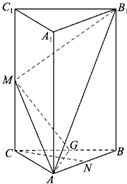 如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点.且CC1=
如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点.且CC1=