题目内容
函数f(x)=x2(ex-1+ax+b),已知x=-2和x=1为y=f′(x)的零点.
(1)求a和b的值;
(2)设g(x)=
x3-x2,证明:对?x∈(-∞,+∞)恒有f(x)-g(x)>0.
(1)求a和b的值;
(2)设g(x)=
| 2 |
| 3 |
考点:利用导数研究函数的单调性,导数的运算
专题:导数的综合应用
分析:(1)先求出函数的导数,得方程组,从而求出a,b的值;
(2)先求出f(x)-g(x)=x2(ex-1-1),令h(x)=ex-1-x,通过求导得出h(x)≥h(1),也就是恒有h(x)≥0,从而证明结论.
(2)先求出f(x)-g(x)=x2(ex-1-1),令h(x)=ex-1-x,通过求导得出h(x)≥h(1),也就是恒有h(x)≥0,从而证明结论.
解答:
解:(1)f'(x)=2ex-1+x2ex-1+3ax2+2bx=xex-1(x+2)+x(3ax+2b),由x=-2和x=1为y=f'(x)的零点知
即
,解得:
.
(2)证明:由(1)得f(x)=x2ex-1-
x3-x2,故f(x)-g(x)=x2ex-1-
x3-x2-
x3+x2=x2(ex-1-x).
令h(x)=ex-1-x,则h'(x)=ex-1-1.
令h'(x)=0,得x=1h'(x)、h(x)随x的变化情况如上表,
由上表可知,当x=1时,h(x)取得极小值,也是最小值;
即当x∈(-∞,+∞)时,h(x)≥h(1),也就是恒有h(x)≥0.
又x2≥0,故对任意x∈(-∞,+∞),恒有f(x)-g(x)≥0.
| x | (-∞,0) | 1 | (1,+∞) |
| h'(x) | - | 0 | + |
| h(x) | ↘ | 0 | ↗ |
|
|
|
(2)证明:由(1)得f(x)=x2ex-1-
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
令h(x)=ex-1-x,则h'(x)=ex-1-1.
令h'(x)=0,得x=1h'(x)、h(x)随x的变化情况如上表,
由上表可知,当x=1时,h(x)取得极小值,也是最小值;
即当x∈(-∞,+∞)时,h(x)≥h(1),也就是恒有h(x)≥0.
又x2≥0,故对任意x∈(-∞,+∞),恒有f(x)-g(x)≥0.
点评:本题考查了函数的单调性,不等式的证明,本题属于中档题.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
曲线y=
x2-2在x=1处的切线的斜率是( )
| 1 |
| 2 |
| A、0 | ||
| B、1 | ||
| C、-1 | ||
D、
|
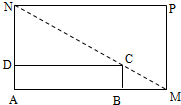 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米.