题目内容
16.在△ABC中,A=120°,AB=4,若点D在边BC上,且$\overrightarrow{BD}$=2$\overrightarrow{DC}$,AD=$\frac{2\sqrt{7}}{3}$,则AC的长.分析 画出图形,结合图形,利用$\overrightarrow{BD}$=2$\overrightarrow{DC}$,得出$\overrightarrow{AD}$-$\overrightarrow{AB}$=2($\overrightarrow{AC}$-$\overrightarrow{AD}$),再利用平面向量的数量积求出|$\overrightarrow{AC}$|即可.
解答 解:如图所示: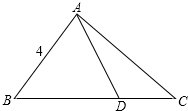
△ABC中,∠BAC=120°,AB=4,点D在边BC上,$\overrightarrow{BD}$=2$\overrightarrow{DC}$,
∴$\overrightarrow{BD}$=$\overrightarrow{AD}$-$\overrightarrow{AB}$,
$\overrightarrow{DC}$=$\overrightarrow{AC}$-$\overrightarrow{AD}$,
∴$\overrightarrow{AD}$-$\overrightarrow{AB}$=2($\overrightarrow{AC}$-$\overrightarrow{AD}$),
∴3$\overrightarrow{AD}$=2$\overrightarrow{AC}$+$\overrightarrow{AB}$,
两边平方得9${\overrightarrow{AD}}^{2}$=4${\overrightarrow{AC}}^{2}$+4$\overrightarrow{AC}$•$\overrightarrow{AB}$+${\overrightarrow{AB}}^{2}$,
又AD=$\frac{2\sqrt{7}}{3}$,
∴9×${(\frac{2\sqrt{7}}{3})}^{2}$=4${\overrightarrow{AC}}^{2}$+4×|$\overrightarrow{AC}$|×4×cos120°+42,
化简得${|\overrightarrow{AC}|}^{2}$-2|$\overrightarrow{AC}$|-3=0,
解得|$\overrightarrow{AC}$|=3或|$\overrightarrow{AC}$|=-1(不合题意舍去),
∴AC的长为3.
点评 本题考查了利用平面向量的线性运算与数量积运算求三角形边长的应用问题,是基础题目

| A. | (-∞,-$\frac{9}{4}$] | B. | (-2,+∞) | C. | [-$\frac{9}{4}$,+∞) | D. | [4,+∞) |
| 气温(℃) | 14 | 12 | 8 | 6 |
| 用电量(度) | 22 | 26 | 34 | 38 |
| A. | 20 | B. | 25 | C. | 30 | D. | 35 |