题目内容
4.在△ABC中,已知a、b、c分别是内角A、B、C的对边,且满足2acosB+ccosB+bcosC=0.(Ⅰ)求角B的大小;
(Ⅱ)若b=$\sqrt{13}$,a+c=4,求△ABC的面积.
分析 (1)使用余弦定理将角化边,整理出a,b,c的关系,代入余弦定理解出cosB;
(2)使用余弦定理解出ac,代入面积公式计算.
解答 解:(1)2acosB+ccosB+bcosC=0,
∴2a×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$+c×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$+b×$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=0,
∴$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{c}+a=0$,即a2+c2-b2=-ac.
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=-$\frac{1}{2}$.
∴B=$\frac{2π}{3}$.
(2)∵a+c=4,∴a2+c2=16-2ac.
∵cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{3-2ac}{2ac}=-\frac{1}{2}$.
解得ac=3.
∴△ABC的面积S=$\frac{1}{2}ac$sinB=$\frac{1}{2}×3×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$.
点评 本题考查了余弦定理在解三角形中额应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知球的内接三棱锥D一ABC,△ABC中,AB⊥AC且AB=AC=2$\sqrt{2}$,DB=DC=4,二面角A-BC-D的大小为$\frac{3π}{4}$,若球内一飞行物(忽略其大小)可以在球内任意飞行,则落在三棱锥D-ABC内的概率为( )
| A. | $\frac{3π}{13}$ | B. | $\frac{8\sqrt{2}}{27π}$ | C. | $\frac{8}{85π}$ | D. | $\frac{9\sqrt{10}}{200π}$ |
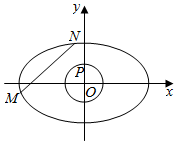 如图,已知椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,圆O:x2+y2=1,其中M,N是椭圆C上的两个动点,P是圆O上一个动点.
如图,已知椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,圆O:x2+y2=1,其中M,N是椭圆C上的两个动点,P是圆O上一个动点.