题目内容
6.计算:(1)sin$\frac{π}{12}$cos$\frac{π}{12}$=$\frac{1}{4}$;
(2)cos105°cos15°=$-\frac{1}{4}$;
(3)sin2$\frac{π}{12}$-cos2$\frac{π}{12}$=$-\frac{\sqrt{3}}{2}$;
(4)$\frac{tan67.5°}{1-ta{n}^{2}67.5°}$=$-\frac{1}{2}$.
分析 (1)直接利用二倍角的正弦化简求值;
(2)利用诱导公式化余弦为正弦,再用二倍角的正弦化简求值;
(3)利用二倍角的余弦化简得答案;
(4)利用二倍角的正切化简得答案.
解答 解:(1)sin$\frac{π}{12}$cos$\frac{π}{12}$=$\frac{1}{2}sin\frac{π}{6}=\frac{1}{2}×\frac{1}{2}=\frac{1}{4}$;
(2)cos105°cos15°=$-sin15°cos15°=-\frac{1}{2}sin30°=-\frac{1}{4}$;
(3)sin2$\frac{π}{12}$-cos2$\frac{π}{12}$═$-(co{s}^{2}\frac{π}{12}-si{n}^{2}\frac{π}{12})=-cos\frac{π}{6}=-\frac{\sqrt{3}}{2}$;
(4)$\frac{tan67.5°}{1-ta{n}^{2}67.5°}$=$\frac{1}{2}\frac{2tan67.5°}{1-ta{n}^{2}67.5°}=\frac{1}{2}tan135°=-\frac{1}{2}tan45°=-\frac{1}{2}$.
故答案为:(1)$\frac{1}{4}$;(2)$-\frac{1}{4}$;(3)$-\frac{\sqrt{3}}{2}$;(4)$-\frac{1}{2}$.
点评 本题考查三角函数的化简求值,考查了三角函数中的恒等变换应用,是基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
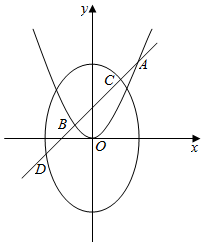 如图,抛物线C1:y=$\frac{1}{4}$x2的焦点F也是椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点,且在两曲线的一个公共点处的直线l1:$\sqrt{6}$x-2y-3=0与C1相切.
如图,抛物线C1:y=$\frac{1}{4}$x2的焦点F也是椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点,且在两曲线的一个公共点处的直线l1:$\sqrt{6}$x-2y-3=0与C1相切.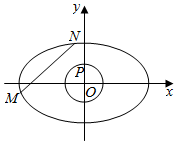 如图,已知椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,圆O:x2+y2=1,其中M,N是椭圆C上的两个动点,P是圆O上一个动点.
如图,已知椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,圆O:x2+y2=1,其中M,N是椭圆C上的两个动点,P是圆O上一个动点.