题目内容
1.已知函数f(x)=4-x+2x与g(x)=4x+2-x-m的图象上存在关于x轴对称的点,则m的取值范围是( )| A. | (-∞,-$\frac{9}{4}$] | B. | (-2,+∞) | C. | [-$\frac{9}{4}$,+∞) | D. | [4,+∞) |
分析 根据对称性质得到m=4-x+2x+4x+2-x,设2x=t,则t>0,则m=$\frac{1}{{t}^{2}}$+t+t2+$\frac{1}{t}$,利用基本不等式即可求出.
解答 解:函数f(x)=4-x+2x与g(x)=4x+2-x-m的图象上存在关于x轴对称的点,
则方程4-x+2x=-(4x+2-x-m)?m=4-x+2x+4x+2-x有解,
设2x=t,则t>0,
∴m=$\frac{1}{{t}^{2}}$+t+t2+$\frac{1}{t}$≥2$\sqrt{t•\frac{1}{t}}$+2$\sqrt{{t}^{2}•\frac{1}{{t}^{2}}}$=2+2=4,当且仅当t=1时取等号,
∴m≥4,
故选:D.
点评 本题考查了构造函数法求方程的解及参数范围以及基本不等式,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
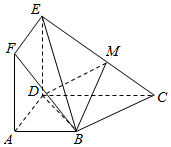 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,$AB=AD=\frac{1}{2}CD=2$,$\overrightarrow{EM}=λ\overrightarrow{EC}(0<λ<1)$.
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,$AB=AD=\frac{1}{2}CD=2$,$\overrightarrow{EM}=λ\overrightarrow{EC}(0<λ<1)$.