题目内容
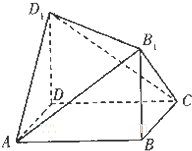如图的几何体是长方体A BCD-A1B1C1D1的一部分，其中A B=AD=3，DD1=BB1=2cm则该几何体的外接球的表面积为（ ）| A、11πcm2 | ||||
| B、22πcm2 | ||||
C、
| ||||
D、11
|
考点：球内接多面体,球的体积和表面积
专题：空间位置关系与距离
分析：易知，长方体的体对角线长就是长方体外接球的直径，依此可使问题获得解决．
解答：
解：易知长方体的体对角线为DB1=
=
=
．
所以外接球的半径R=
，所以S=4πR2=4π×
=22π（cm2）
故选B
| AD2+DC2+BB12 |
| 32+32+22 |
| 22 |
所以外接球的半径R=
| ||
| 2 |
| 22 |
| 4 |
故选B
点评：本题考查了长方体与其外接球的关系，抓住长方体的体对角线为其外接球的直径是关键．
练习册系列答案
相关题目
在平面直角坐标系n∈N+，n≥2）中，设A（-2，3），B（3，-2），沿x轴把直角坐标平面折成大小为
的二面角后，则线段AB的长度是（ ）
| 2π |
| 3 |
A、
| ||||||||
B、2
| ||||||||
C、3
| ||||||||
D、[
|
已知四棱锥P-ABCD，PC⊥底面ABCD，PC=2，且底面ABCD是边长为1的正方形，E是侧棱PC上的 一点，点F在线段BD上，且满足DF=3BF，若EF∥平面PAB．