题目内容
截止2012年年底,已知某市人口数为80万,若今后能将人口年平均增长率控制在1%,经过x年以后此市人口数为y(万).
(1)求y与x的函数关系y=f(x);
(2)求函数y=f(x)的定义域;
(3)判断函数f(x)是增函数还是减函数?
(1)求y与x的函数关系y=f(x);
(2)求函数y=f(x)的定义域;
(3)判断函数f(x)是增函数还是减函数?
考点:根据实际问题选择函数类型,函数单调性的判断与证明
专题:应用题,函数的性质及应用
分析:(1)由题意,函数模型应该选择指数函数型,故y=80(1+1%)x=80×1.01x,(x∈N);
(2)根据实际问题确定定义域;
(3)由指数函数的性质确定单调性.
(2)根据实际问题确定定义域;
(3)由指数函数的性质确定单调性.
解答:
解:(1)由题意,y=80(1+1%)x=80×1.01x,(x∈N);
(2)函数y=f(x)的定义域为N;
(3)由指数函数的性质知,
函数f(x)是增函数.
(2)函数y=f(x)的定义域为N;
(3)由指数函数的性质知,
函数f(x)是增函数.
点评:本题考查了函数在实际问题中的应用,同时考查了指数函数的性质,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
若抛物线y2=2px(p>0)上横坐标是2的点M到抛物线焦点距离是3,则p=( )
| A、1 | B、2 | C、4 | D、8 |
抛物线x=ay2的准线方程是x=2,则a的值为( )
| A、-8 | ||
B、-
| ||
C、
| ||
| D、8 |
在四面体PABC中,PA、PB、PC两两垂直,且均相等,E是AB的中点,则异面直线AC与PE所成的角为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
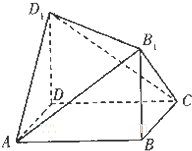 如图的几何体是长方体A BCD-A1B1C1D1的一部分,其中A B=AD=3,DD1=BB1=2cm则该几何体的外接球的表面积为( )
如图的几何体是长方体A BCD-A1B1C1D1的一部分,其中A B=AD=3,DD1=BB1=2cm则该几何体的外接球的表面积为( )| A、11πcm2 | ||||
| B、22πcm2 | ||||
C、
| ||||
D、11
|
过椭圆
+
=1的中心任作一直线交椭圆于P、Q两点,F是椭圆的一个焦点,则△PQF周长的最小值是( )
| x2 |
| 25 |
| y2 |
| 16 |
| A、14 | B、16 | C、18 | D、20 |