题目内容
已知点A(2,0),B(3,1).
①动点M在曲线y2=8x上移动时,求|MA|+|MB|的最小值;
②动点M在曲线
+
=1上移动时,求2|MA|+|MB|的最小值;
③动点M在曲线
-y2=1上移动时,求|
MA|+|MB|的最小值.
①动点M在曲线y2=8x上移动时,求|MA|+|MB|的最小值;
②动点M在曲线
| x2 |
| 16 |
| y2 |
| 12 |
③动点M在曲线
| x2 |
| 3 |
| ||
| 2 |
考点:抛物线的简单性质,椭圆的简单性质,双曲线的简单性质
专题:计算题,作图题,圆锥曲线的定义、性质与方程
分析:分别用抛物线的定义,椭圆的第二定义,双曲线的第二定义求解.
解答:
解:①曲线y2=8x的焦点为A(2,0),准线为x=-2,如图,
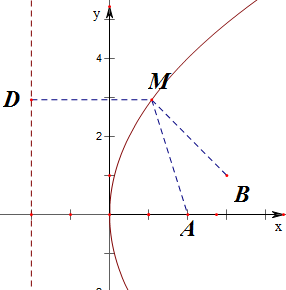
|MA|+|MB|=|MD|+|MB|;
故|MA|+|MB|的最小值是点B到直线x=-2的距离3+2=5;
②椭圆
+
=1的右焦点为A(2,0),右准线为x=8,如下图,

2|MA|+|MB|=|MB|+|MC|;
2|MA|+|MB|的最小值为点B到直线x=8的距离8-3=5;
③双曲线
-y2=1的右焦点为A(2,0),右准线为x=
,如下图,

=
;|
MA|=|MC|;
故|
MA|+|MB|=|MC|+|MB|;
故|
MA|+|MB|的最小值为点B到直线x=
的距离为3-
=
.

|MA|+|MB|=|MD|+|MB|;
故|MA|+|MB|的最小值是点B到直线x=-2的距离3+2=5;
②椭圆
| x2 |
| 16 |
| y2 |
| 12 |

2|MA|+|MB|=|MB|+|MC|;
2|MA|+|MB|的最小值为点B到直线x=8的距离8-3=5;
③双曲线
| x2 |
| 3 |
| 3 |
| 2 |

| |MA| |
| |MC| |
| 2 | ||
|
| ||
| 2 |
故|
| ||
| 2 |
故|
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查了抛物线的定义,椭圆的第二定义,双曲线的第二定义,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
抛物线x=ay2的准线方程是x=2,则a的值为( )
| A、-8 | ||
B、-
| ||
C、
| ||
| D、8 |
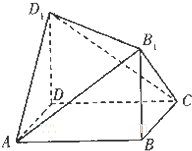 如图的几何体是长方体A BCD-A1B1C1D1的一部分,其中A B=AD=3,DD1=BB1=2cm则该几何体的外接球的表面积为( )
如图的几何体是长方体A BCD-A1B1C1D1的一部分,其中A B=AD=3,DD1=BB1=2cm则该几何体的外接球的表面积为( )| A、11πcm2 | ||||
| B、22πcm2 | ||||
C、
| ||||
D、11
|
过椭圆
+
=1的中心任作一直线交椭圆于P、Q两点,F是椭圆的一个焦点,则△PQF周长的最小值是( )
| x2 |
| 25 |
| y2 |
| 16 |
| A、14 | B、16 | C、18 | D、20 |
下面对程序框图中的图形符号的说法错误的是( )
| A、起、止框是任何流程不可少的,表明程序开始和结束 |
| B、输入、输出可用在算法中任何需要输入、输出的位置 |
| C、算法中间要处理数据或计算,可分别写在不同的注释框内 |
| D、当算法要求对两个不同的结果进行判断时,判断条件要写在判断框内 |