题目内容
设a，b，c∈（0，+∞），且a+b+c=1，求证（1-a）（1-b）（1-c）≥8abc．
考点：基本不等式
专题：不等式的解法及应用
分析：由基本不等式可得1-a=b+c≥2
，1-b=a+c≥2
，1-c=a+b≥2
，由不等式的性质三个不等式相乘可得．
| bc |
| ac |
| ab |
解答：
证明：∵a+b+c=1，a，b，c都是正数；
∴1-a=b+c≥2
，当且仅当b=c时取等号；
同理可得1-b=a+c≥2
，当且仅当a=c时取等号；
1-c=a+b≥2
，当且仅当a=b时取等号；
∴（1-a）（1-b）（1-c）≥8abc，当且仅当a=b=c时取等号．
∴1-a=b+c≥2
| bc |
同理可得1-b=a+c≥2
| ac |
1-c=a+b≥2
| ab |
∴（1-a）（1-b）（1-c）≥8abc，当且仅当a=b=c时取等号．
点评：本题考查基本不等式和不等式的性质，属基础题．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
若抛物线y2=2px（p＞0）上横坐标是2的点M到抛物线焦点距离是3，则p=（ ）
| A、1 | B、2 | C、4 | D、8 |
抛物线x=ay2的准线方程是x=2，则a的值为（ ）
| A、-8 | ||
B、-
| ||
C、
| ||
| D、8 |
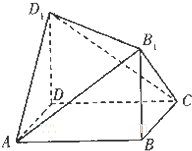如图的几何体是长方体A BCD-A1B1C1D1的一部分，其中A B=AD=3，DD1=BB1=2cm则该几何体的外接球的表面积为（ ）| A、11πcm2 | ||||
| B、22πcm2 | ||||
C、
| ||||
D、11
|