题目内容
在平面直角坐标系n∈N+,n≥2)中,设A(-2,3),B(3,-2),沿x轴把直角坐标平面折成大小为
的二面角后,则线段AB的长度是( )
| 2π |
| 3 |
A、
| ||||||||
B、2
| ||||||||
C、3
| ||||||||
D、[
|
考点:二面角的平面角及求法
专题:空间位置关系与距离
分析:作AC⊥x轴于C,BD⊥x轴于D,则
=
+
+
,由此能求出线段AB的长度.
| AB |
| AC |
| CD |
| DB |
解答:
 解:作AC⊥x轴于C,BD⊥x轴于D,
解:作AC⊥x轴于C,BD⊥x轴于D,
则
=
+
+
,
∵A(-2,3),B(3,-2),∴C(-2,0),D(3,0),
∴|
|=3,|
|=5,|
|=2,
•
=0,
•
=0,
•
=2×3×cos(π-
)=3,
∴
2=(
+
+
)2
=9+25+4+2×3=44,
∴|
|=
=2
.
故选:B.
 解:作AC⊥x轴于C,BD⊥x轴于D,
解:作AC⊥x轴于C,BD⊥x轴于D,则
| AB |
| AC |
| CD |
| DB |
∵A(-2,3),B(3,-2),∴C(-2,0),D(3,0),
∴|
| AC |
| CD |
| DB |
| AC |
| CD |
| CD |
| DB |
| DB |
| AC |
| 2π |
| 3 |
∴
| AB |
| AC |
| CD |
| DB |
=9+25+4+2×3=44,
∴|
| AB |
| 44 |
| 11 |
故选:B.
点评:本题考查线段长的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
在四面体PABC中,PA、PB、PC两两垂直,且均相等,E是AB的中点,则异面直线AC与PE所成的角为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
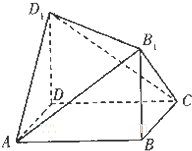 如图的几何体是长方体A BCD-A1B1C1D1的一部分,其中A B=AD=3,DD1=BB1=2cm则该几何体的外接球的表面积为( )
如图的几何体是长方体A BCD-A1B1C1D1的一部分,其中A B=AD=3,DD1=BB1=2cm则该几何体的外接球的表面积为( )| A、11πcm2 | ||||
| B、22πcm2 | ||||
C、
| ||||
D、11
|
利用秦九韶算法计算f(x)=x5+2x4+3x3+4x2+5x+6在x=5时的值为( )
| A、4881 | B、220 |
| C、975 | D、4818 |