题目内容
已知椭圆E的中心在原点,左焦点为(-
,0),且经过点M(4,1).
(1)求椭圆E的方程;
(2)若斜率为1的直线l(不过点M)交椭圆E于不同的两点A,B,求证:直线MA、MB与x轴围成一个等腰三角形.
| 15 |
(1)求椭圆E的方程;
(2)若斜率为1的直线l(不过点M)交椭圆E于不同的两点A,B,求证:直线MA、MB与x轴围成一个等腰三角形.
考点:椭圆的简单性质
专题:计算题,圆锥曲线中的最值与范围问题
分析:(1)设椭圆的方程为
+
=1,从而可得a2-b2=15,
+
=1,从而解得;
(2)由题可设直线l方程为y=x+m;直线MA,MB的斜率分别为k1,k2;要证直线MA、MB与x轴围成一个等腰三角形,只要证明k1+k2=0;从而证明.
| x2 |
| a2 |
| y2 |
| b2 |
| 16 |
| a2 |
| 1 |
| b2 |
(2)由题可设直线l方程为y=x+m;直线MA,MB的斜率分别为k1,k2;要证直线MA、MB与x轴围成一个等腰三角形,只要证明k1+k2=0;从而证明.
解答:
解:(1)设椭圆的方程为
+
=1,
∵c=
,∴a2-b2=15;
又∵
+
=1;
故a2=20,b2=5;
故椭圆E的方程为
+
=1;
(2)证明:由题可设直线l方程为y=x+m;直线MA,MB的斜率分别为k1,k2;
将方程y=x+m代入
+
=1整理得,
5x2+8mx+4m2-20=0;
△=64m2-20(4m2-5)>0,
解得,-5<m<5;
要证直线MA、MB与x轴围成一个等腰三角形,
只要证明k1+k2=0;
设A(x1,y1),B(x2,y2);
则x1+x2=-
,x1x2=
;
故k1+k2=
+
=
;
而(y1-1)(x2-4)+(y2-1)(x1-4)
=(x1+m-1)(x2-4)+(x2+m-1)(x1-4)
=2x2x1+(m-5)(x1+x2)-8(m-1)
=2
-(m-5)
-8(m-1)=0;
故k1+k2=0.
| x2 |
| a2 |
| y2 |
| b2 |
∵c=
| 15 |
又∵
| 16 |
| a2 |
| 1 |
| b2 |
故a2=20,b2=5;
故椭圆E的方程为
| x2 |
| 20 |
| y2 |
| 5 |
(2)证明:由题可设直线l方程为y=x+m;直线MA,MB的斜率分别为k1,k2;
将方程y=x+m代入
| x2 |
| 20 |
| y2 |
| 5 |
5x2+8mx+4m2-20=0;
△=64m2-20(4m2-5)>0,
解得,-5<m<5;
要证直线MA、MB与x轴围成一个等腰三角形,
只要证明k1+k2=0;
设A(x1,y1),B(x2,y2);
则x1+x2=-
| 8m |
| 5 |
| 4m2-20 |
| 5 |
故k1+k2=
| y1-1 |
| x1-4 |
| y2-1 |
| x2-4 |
=
| (y1-1)(x2-4)+(y2-1)(x1-4) |
| (x1-4)(x2-4) |
而(y1-1)(x2-4)+(y2-1)(x1-4)
=(x1+m-1)(x2-4)+(x2+m-1)(x1-4)
=2x2x1+(m-5)(x1+x2)-8(m-1)
=2
| 4m2-20 |
| 5 |
| 8m |
| 5 |
故k1+k2=0.
点评:本题考查了圆锥曲线与直线方程联立求解,化简比较困难,属于中档题.

练习册系列答案
相关题目
若抛物线y2=2px(p>0)上横坐标是2的点M到抛物线焦点距离是3,则p=( )
| A、1 | B、2 | C、4 | D、8 |
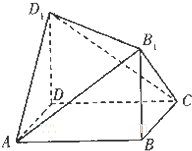 如图的几何体是长方体A BCD-A1B1C1D1的一部分,其中A B=AD=3,DD1=BB1=2cm则该几何体的外接球的表面积为( )
如图的几何体是长方体A BCD-A1B1C1D1的一部分,其中A B=AD=3,DD1=BB1=2cm则该几何体的外接球的表面积为( )| A、11πcm2 | ||||
| B、22πcm2 | ||||
C、
| ||||
D、11
|
过椭圆
+
=1的中心任作一直线交椭圆于P、Q两点,F是椭圆的一个焦点,则△PQF周长的最小值是( )
| x2 |
| 25 |
| y2 |
| 16 |
| A、14 | B、16 | C、18 | D、20 |