题目内容
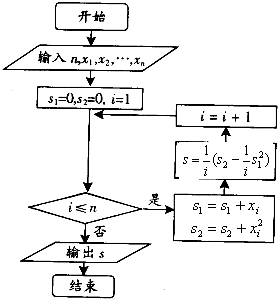 某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,x2,…,xn(单位:吨),根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的s结果为( )
某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,x2,…,xn(单位:吨),根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的s结果为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:程序框图
专题:算法和程序框图
分析:n=2,且x1,x2分别为1,2,执行程序框图,写出每次循环s1,s2,s的值,当i<=n时,计算S的值并输出即可.
解答:
解:执行程序框图,有
n=2,x1=1,x2=2,s1=0,s2=0,i=1
i≤n条件成立,执行循环体,
s1=s1+x1=1
s2=s2+x12=1
S=0
i=2
i≤n条件成立,执行循环体,
s1=s1+x2=3
s2=s2+x22=5
S=
i=3
i≤n条件不成立,输出S的值为
,
故选:A.
n=2,x1=1,x2=2,s1=0,s2=0,i=1
i≤n条件成立,执行循环体,
s1=s1+x1=1
s2=s2+x12=1
S=0
i=2
i≤n条件成立,执行循环体,
s1=s1+x2=3
s2=s2+x22=5
S=
| 1 |
| 4 |
i=3
i≤n条件不成立,输出S的值为
| 1 |
| 4 |
故选:A.
点评:本题主要考察程序框图和算法,属于基础题.

练习册系列答案
相关题目
已知定义在R上的函数f(x)满足f(x+2)=-f(x),当x∈(-1,3]时,f(x)=
,其中t>0,若方程f(x)=
恰有3个不同的实数根,则t的取值范围为( )
|
| x |
| 3 |
A、(0,
| ||
B、(
| ||
C、(
| ||
D、(
|
下列函数中,在其定义域是减函数的是( )
| A、f(x)=-x2+2x+1 | ||
B、f(x)=
| ||
C、f(x)=(
| ||
| D、f(x)=ln(2-x) |
若y=f(x)的定义域是[-1,2],则函数f(x-1)+f(2x+1)的定义域是( )
A、[-2,
| ||
B、[-1,
| ||
| C、[0,1] | ||
D、[0,
|
已知△ABC中,a、b、c是角A、B、C所对的边,若B=45°,a=
,b=2,那么角A等于( )
| 2 |
| A、30°或150° |
| B、60°或120° |
| C、60° |
| D、30° |