题目内容
下列函数中，在其定义域是减函数的是（ ）
| A、f（x）=-x2+2x+1 | ||
B、f（x）=
| ||
C、f(x)=(
| ||
| D、f（x）=ln（2-x） |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：根据二次函数的单调性，反比例函数的单调性，指数函数的单调性，含绝对值函数的单调性，对数函数的单调性及单调性的定义即可找出正确的选项．
解答：
解：A．该函数为二次函数，在其定义域上没有单调性；
B．该函数为反比例函数，在其定义域上没有单调性；
C．f（x）=(
)|x|=
，∴x＜0时f（x）是增函数，即在其定义域上不是减函数；
D．f（x）在定义域（-∞，2）上，x增大时，f（x）减小，所以该函数在其定义域上是减函数．
故选D．
B．该函数为反比例函数，在其定义域上没有单调性；
C．f（x）=(
| 1 |
| 4 |
|
D．f（x）在定义域（-∞，2）上，x增大时，f（x）减小，所以该函数在其定义域上是减函数．
故选D．
点评：考查二次函数、反比例函数、含绝对值函数在其定义域上的单调性，对数函数的单调性及单调性的定义．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
过抛物线的焦点F作互相垂直的两条直线，分别交准线于P、Q两点，又过P、Q分别作抛物线对称轴OF的平行线，交抛物线于M、N两点，则M、N、F三点（ ）
| A、共圆 | B、共线 |
| C、在另一抛物线上 | D、在一双曲线上 |
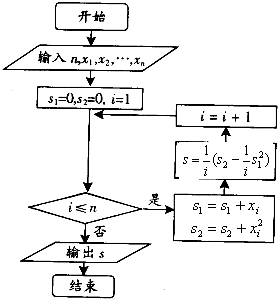某城市缺水问题比较突出，为了制定节水管理办法，对全市居民某年的月均用水量进行了抽样调查，其中n位居民的月均用水量分别为x1，x2，…，xn（单位：吨），根据如图所示的程序框图，若n=2，且x1，x2分别为1，2，则输出的s结果为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={0，1，2，3，4}，B={2，4，8}，那么A∩B子集的个数是（ ）
| A、4 | B、5 | C、7 | D、8 |