题目内容
函数f（x）=2sin（ωx+φ）-1，x∈R，其值域为 ．
考点：三角函数的最值,正弦函数的定义域和值域
专题：三角函数的图像与性质
分析：直接利用正弦函数的值域，求解即可．
解答：
解：∵x∈R，
∴ωx+φ∈R，
∴sin（ωx+φ）∈[-1，1]，
∴2sin（ωx+φ）-1∈[-3，1]．
故答案为：[-3，1]．
∴ωx+φ∈R，
∴sin（ωx+φ）∈[-1，1]，
∴2sin（ωx+φ）-1∈[-3，1]．
故答案为：[-3，1]．
点评：本题考查三角函数的最值，正弦函数的值域的求法，考查计算能力．
练习册系列答案
相关题目
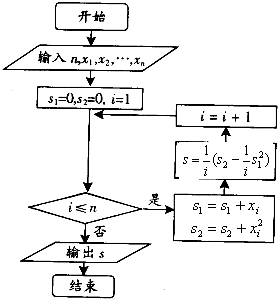某城市缺水问题比较突出，为了制定节水管理办法，对全市居民某年的月均用水量进行了抽样调查，其中n位居民的月均用水量分别为x1，x2，…，xn（单位：吨），根据如图所示的程序框图，若n=2，且x1，x2分别为1，2，则输出的s结果为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
“k=±
”是“直线x-y+k=0与圆x2+y2=1相切”的（ ）
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也也必要条件 |
下列函数既是奇函数又是减函数的是（ ）
| A、f（x）=x3 | ||
| B、f（x）=sinx | ||
C、f（x）=
| ||
| D、f（x）=-x|x| |
已知集合A={0，1，2，3，4}，B={2，4，8}，那么A∩B子集的个数是（ ）
| A、4 | B、5 | C、7 | D、8 |