题目内容
已知定义在R上的函数f(x)满足f(x+2)=-f(x),当x∈(-1,3]时,f(x)=
,其中t>0,若方程f(x)=
恰有3个不同的实数根,则t的取值范围为( )
|
| x |
| 3 |
A、(0,
| ||
B、(
| ||
C、(
| ||
D、(
|
考点:根的存在性及根的个数判断,函数的周期性
专题:计算题,函数的性质及应用
分析:确定f(x)的周期为4,x∈(5,6)时,f(x)=t(x-5),x∈(6,7)时,f(x)=t(7-x),再利用t>0,f(x)=
恰有3个不同的实数根,可得t(2-1)>
,t(6-1)<2,即可求出t的取值范围.
| x |
| 3 |
| 2 |
| 3 |
解答:
解:由f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x),故f(x)的周期为4,
∵x∈(1,2)时,f(x)=t(x-1),x∈(2,3)时,f(x)=t(3-x),
∴x∈(5,6)时,f(x)=t(x-5),x∈(6,7)时,f(x)=t(7-x),
∵t>0,f(x)=
恰有3个不同的实数根,
∴t(2-1)>
,t(6-1)<2
∴2>t>
,
故选:B.
∴f(x+4)=-f(x+2)=f(x),故f(x)的周期为4,
∵x∈(1,2)时,f(x)=t(x-1),x∈(2,3)时,f(x)=t(3-x),
∴x∈(5,6)时,f(x)=t(x-5),x∈(6,7)时,f(x)=t(7-x),
∵t>0,f(x)=
| x |
| 3 |
∴t(2-1)>
| 2 |
| 3 |
∴2>t>
| 2 |
| 3 |
故选:B.
点评:本题考查函数的周期性、根的存在性及根的个数判断,考查学生的计算能力,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
过抛物线的焦点F作互相垂直的两条直线,分别交准线于P、Q两点,又过P、Q分别作抛物线对称轴OF的平行线,交抛物线于M、N两点,则M、N、F三点( )
| A、共圆 | B、共线 |
| C、在另一抛物线上 | D、在一双曲线上 |
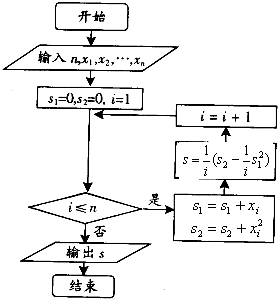 某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,x2,…,xn(单位:吨),根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的s结果为( )
某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,x2,…,xn(单位:吨),根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的s结果为( )A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数既是奇函数又是减函数的是( )
| A、f(x)=x3 | ||
| B、f(x)=sinx | ||
C、f(x)=
| ||
| D、f(x)=-x|x| |
