题目内容
定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.
已知函数f(x)=1+a•(
)x+(
)x,
(1)当a=-
时,求函数f(x)在(-∞,0)上的值域,并判断函数f(x)在(-∞,0)上是否为有界函数,请说明理由;
(2)若函数f(x)在[0,+∞)上是以4为上界的有界函数,求实数a的取值范围.
已知函数f(x)=1+a•(
| 1 |
| 3 |
| 1 |
| 9 |
(1)当a=-
| 1 |
| 2 |
(2)若函数f(x)在[0,+∞)上是以4为上界的有界函数,求实数a的取值范围.
考点:函数的值域
专题:函数的性质及应用
分析:(1)把a=-
代入函数的表达式,得出函数的单调区间,结合有界函数的定义进行判断;
(2)由题意知,|f(x)|≤4对x∈[0,+∞)恒成立.令t=(
)x,-(t+
)≤a≤
-t对t∈(0,1]恒成立,设h(t)=-(t+
),p(t)=
-t,求出单调区间,得到函数的最值,从而求出a的值.
| 1 |
| 2 |
(2)由题意知,|f(x)|≤4对x∈[0,+∞)恒成立.令t=(
| 1 |
| 3 |
| 5 |
| t |
| 3 |
| t |
| 5 |
| t |
| 3 |
| t |
解答:
解:(1)当a=-
时,f(x)=1-
(
)x+(
)x,令t=(
)x,
∵x<0,∴t>1,y=1-
t+t2;
∵y=1-
t+t2在(1,+∞)上单调递增,
∴y>
,即f(x)在(-∞,1)的值域为(
,+∞),
故不存在常数M>0,使|f(x)|≤M成立,
∴函数f(x)在(-∞,0)上不是有界函数;
(2)由题意知,|f(x)|≤4对x∈[0,+∞)恒成立.
即:-4≤f(x)≤4,令t=(
)x,
∵x≥0,∴t∈(0,1]
∴-(t+
)≤a≤
-t对t∈(0,1]恒成立,
∴[-(t+
)]max≤a≤(
-t)min,
设h(t)=-(t+
),p(t)=
-t,由t∈(0,1],
由于h(t)在t∈(0,1]上递增,P(t)在t∈(0,1]上递减,
H(t)在t∈(0,1]上的最大值为h(1)=-6,
P(t)在[1,+∞)上的最小值为p(1)=2
∴实数a的取值范围为[-6,2].
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
∵x<0,∴t>1,y=1-
| 1 |
| 2 |
∵y=1-
| 1 |
| 2 |
∴y>
| 3 |
| 2 |
| 3 |
| 2 |
故不存在常数M>0,使|f(x)|≤M成立,
∴函数f(x)在(-∞,0)上不是有界函数;
(2)由题意知,|f(x)|≤4对x∈[0,+∞)恒成立.
即:-4≤f(x)≤4,令t=(
| 1 |
| 3 |
∵x≥0,∴t∈(0,1]
∴-(t+
| 5 |
| t |
| 3 |
| t |
∴[-(t+
| 5 |
| t |
| 3 |
| t |
设h(t)=-(t+
| 5 |
| t |
| 3 |
| t |
由于h(t)在t∈(0,1]上递增,P(t)在t∈(0,1]上递减,
H(t)在t∈(0,1]上的最大值为h(1)=-6,
P(t)在[1,+∞)上的最小值为p(1)=2
∴实数a的取值范围为[-6,2].
点评:本题考查了函数的值域问题,考查了新定义问题,考查了函数的单调性,函数的最值问题,是一道综合题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
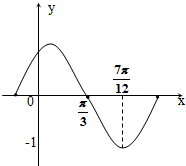
y=sin(ωx+ϕ)(ω>0,|ϕ|<
)的图象的一部分图形如图所示,则函数的解析式为( )
| π |
| 2 |

A、y=sin(x+
| ||
B、y=sin(x-
| ||
C、y=sin(2x+
| ||
D、y=sin(2x-
|
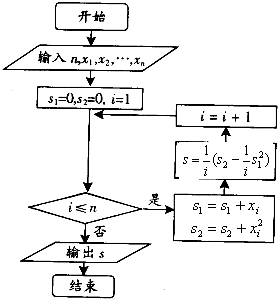 某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,x2,…,xn(单位:吨),根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的s结果为( )
某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,x2,…,xn(单位:吨),根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的s结果为( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)是奇函数,当x>0时,f(x)=-x(1+2x);当x<0时,f(x)等于( )
| A、-x(1+2x) |
| B、x(1+2x) |
| C、x(1-2x) |
| D、-x(1-2x) |
