题目内容
下列说法中:
①若f(x)=ax2+(2a+b)x+2(其中x∈[2a-1,a+4])是偶函数,则实数b=2;
②f(x)=
+
既是奇函数又是偶函数;
③已知f(x)是定义在R上的奇函数,若当x∈[0,+∞)时,f(x)=x(1+x),则当x∈R时,f(x)=x(1+|x|);
④已知f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R都满足f(x•y)=x•f(y)+y•f(x),则f(x)是奇函数.
其中正确说法的序号是 .
①若f(x)=ax2+(2a+b)x+2(其中x∈[2a-1,a+4])是偶函数,则实数b=2;
②f(x)=
| 2013-x2 |
| x2-2013 |
③已知f(x)是定义在R上的奇函数,若当x∈[0,+∞)时,f(x)=x(1+x),则当x∈R时,f(x)=x(1+|x|);
④已知f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R都满足f(x•y)=x•f(y)+y•f(x),则f(x)是奇函数.
其中正确说法的序号是
考点:函数奇偶性的性质
专题:函数的性质及应用,简易逻辑
分析:①由区间对称性求得a,再由函数为偶函数求得b的值判断;
②由两个根式内部的代数式互为相反数化简后判断;
③当x<0时,-x>0,f(x)═-f(-x)=-[-x(1-x)]=x(1-x)=x(1+|x|),由此判断命题的真假;
④构造f(-x)和f(x)之间的关系式,看符合奇函数还是偶函数,先赋值求出f(-1),再令a=-1,b=x即可说明结论正确.
②由两个根式内部的代数式互为相反数化简后判断;
③当x<0时,-x>0,f(x)═-f(-x)=-[-x(1-x)]=x(1-x)=x(1+|x|),由此判断命题的真假;
④构造f(-x)和f(x)之间的关系式,看符合奇函数还是偶函数,先赋值求出f(-1),再令a=-1,b=x即可说明结论正确.
解答:
解:对于①,由f(x)=ax2+(2a+b)x+2(其中x∈[2a-1,a+4])是偶函数,
则a+4=-2a+1,解得a=-1,f(x)=-x2+(b-2)x+2,且b-2=0,则b=2,命题①正确;
对于②,由
,得x=±
,且f(x)=
+
=0,
∴f(x)=
+
既是奇函数又是偶函数,命题②正确;
对于③,已知f(x)是定义在R上的奇函数,若当x∈[0,+∞)时,f(x)=x(1+x),
则当x<0时,-x>0,f(x)=-f(-x)=-[-x(1-x)]=x(1-x).
∴当x∈R时,f(x)=x(1+|x|),命题③正确;
对于④,已知f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R都满足
f(x•y)=x•f(y)+y•f(x),
∵f(1)=f[(-1)2]=-f(-1)-f(-1)=0,∴f(-1)=0.
令x=-1,y=x,则f(-x)=f(-1•x)=-f(x)+xf(-1)=-f(x),
因此f(x)是奇函数,命题④正确.
故答案为:①②③④.
则a+4=-2a+1,解得a=-1,f(x)=-x2+(b-2)x+2,且b-2=0,则b=2,命题①正确;
对于②,由
|
| 2013 |
| 2013-x2 |
| x2-2013 |
∴f(x)=
| 2013-x2 |
| x2-2013 |
对于③,已知f(x)是定义在R上的奇函数,若当x∈[0,+∞)时,f(x)=x(1+x),
则当x<0时,-x>0,f(x)=-f(-x)=-[-x(1-x)]=x(1-x).
∴当x∈R时,f(x)=x(1+|x|),命题③正确;
对于④,已知f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R都满足
f(x•y)=x•f(y)+y•f(x),
∵f(1)=f[(-1)2]=-f(-1)-f(-1)=0,∴f(-1)=0.
令x=-1,y=x,则f(-x)=f(-1•x)=-f(x)+xf(-1)=-f(x),
因此f(x)是奇函数,命题④正确.
故答案为:①②③④.
点评:本题考查了命题的真假判断与应用,考查了函数奇偶性的性质,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,a、b,c是角A,B,C所对的边,若sinA+sin(C-B)=sin2B,且
<cosB,则△ABC的形状为( )
| c |
| a |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
y=sin(ωx+ϕ)(ω>0,|ϕ|<
)的图象的一部分图形如图所示,则函数的解析式为( )
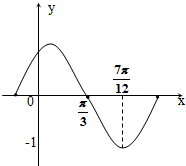
| π |
| 2 |

A、y=sin(x+
| ||
B、y=sin(x-
| ||
C、y=sin(2x+
| ||
D、y=sin(2x-
|
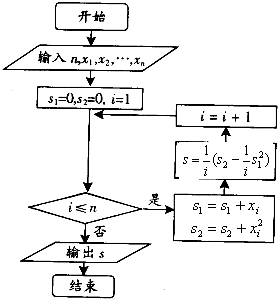 某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,x2,…,xn(单位:吨),根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的s结果为( )
某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,x2,…,xn(单位:吨),根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的s结果为( )