对任意实数x.不等式|x-a|＜|x|＜|x+1|恒成立.则a的取值范围是．题目和参考答案——青夏教育精英家教网—

题目内容

对任意实数x，不等式|x-a|＜|x|＜|x+1|恒成立，则a的取值范围是

．

考点：绝对值不等式的解法

专题：不等式的解法及应用

分析：依题意，当x=0时，不等式|x-a|＜|x|＜|x+1|也成立，即|a|＜0＜1成立，这不可能，从而可得a的取值范围．

解答： 解：∵对任意实数x，不等式|x-a|＜|x|＜|x+1|恒成立，
∴当x=0时，不等式|x-a|＜|x|＜|x+1|也成立，即|a|＜0＜1成立，这样的实数a不存在，
故a的取值范围是∅，
故答案为：∅．

点评：本题考查绝对值不等式的解法，依题意，利用特值法得到|a|＜0＜1成立是关键，考查分析问题、解决问题的能力，属于中档题．

练习册系列答案

相关题目

已知函数f（2x-1）的定义域是[-2，3]，则函数f（x+1）的定义域是

已知数列{a_n}的前n项和为S_n，向量

=（S_n，p²-a），

=（1，p-1）（n∈N^*），满足

∥

．（其中p为正常数，且p≠1）
（1）求数列{a_n}的通项公式；
（2）若p=

，数列{b_n}对任意n∈N^*，都有b₁a_n+b₂a_n-1+b₃a_n-2+…+b_na₁=（n²-n+1）•(

)n+1成立，问数列{b_n}中是否存在最大项？若存在，最大项是第几项；若不存在，说明理由．

在抛物线y=x²上关于直线y=x+3对称两点M，N的坐标分别为

|，若存在直线l₁，l₂与函数y=f（x），x∈（0，4）的图象相切，l₁⊥l₂，则实数a的取值范围为

．

已知函数f（x）=x-a-alnx（a∈R）．
（Ⅰ）当函数y=f（x）有两个零点时，求实数a的取值范围；
（Ⅱ）当函数y=f（x）有两个零点x₁，x₂∈[

，

]且x₁＜x₂时，证明：
①若x₂-x₁≤1，则有

随着a的增大而增大；
③x₁x₂＞1；
（Ⅲ）证明：

k=1

1+lnk

＞ln（n+1），（n∈N^*）．

已知10件产品中有3件次品，现任意抽取4件产品检验，则：
（1）其中恰有1件正品的概率是多少？
（2）其中最多有2件正品的概率是多少？

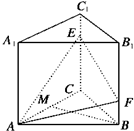如图，在正三棱柱ABC-A₁B₁C₁中，点E，F分别是棱CC₁、BB₁上的点，点M是线段AC上的动点，且满足EC=AB=2BF=2cm，当点M在什么位置时，MB∥平面AEF？并求截面AEF的面积．

试题分类