题目内容
已知10件产品中有3件次品,现任意抽取4件产品检验,则:
(1)其中恰有1件正品的概率是多少?
(2)其中最多有2件正品的概率是多少?
(1)其中恰有1件正品的概率是多少?
(2)其中最多有2件正品的概率是多少?
考点:n次独立重复试验中恰好发生k次的概率
专题:概率与统计
分析:(1)共有
=210种结果,其中恰有1件正品的有
=7,运用古典概率求解即可,
(2)最多有2件正品的有210-7-
=210-7-63=140,运用古典概率公式求解即可.
| C | 4 10 |
| C | 1 7 |
| ×C | 3 3 |
(2)最多有2件正品的有210-7-
| C | 2 7 |
| C | 2 3 |
解答:
解:∵10件产品中有3件次品,现任意抽取4件产品检验,
∴共有
=210种结果,
(1)∵其中恰有1件正品的有
=7,
∴其中恰有1件正品的概率是
=
,
(2)∵最多有2件正品的有210-7-
=210-7-63=140,
∴其中最多有2件正品的概率是
=
,
∴共有
| C | 4 10 |
(1)∵其中恰有1件正品的有
| C | 1 7 |
| ×C | 3 3 |
∴其中恰有1件正品的概率是
| 7 |
| 210 |
| 1 |
| 30 |
(2)∵最多有2件正品的有210-7-
| C | 2 7 |
| C | 2 3 |
∴其中最多有2件正品的概率是
| 140 |
| 210 |
| 2 |
| 3 |
点评:本题考查了古典概率的求解,关键是求解基本事件的个数,所求事件的个数.

练习册系列答案
相关题目
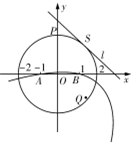 如图,已知圆O:x2+y2=4与y轴正半轴交于点P,A(-1,0),B(1,0),直线l与圆O切于点S(l不垂直于x轴),抛物线过A、B两点且以l为准线.
如图,已知圆O:x2+y2=4与y轴正半轴交于点P,A(-1,0),B(1,0),直线l与圆O切于点S(l不垂直于x轴),抛物线过A、B两点且以l为准线.