题目内容
定义:对函数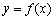 ,对给定的正整数
,对给定的正整数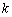 ,若在其定义域内存在实数
,若在其定义域内存在实数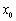 ,使得
,使得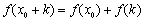 ,则称函数
,则称函数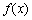 为“
为“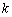 性质函数”。
性质函数”。
(1) 若函数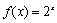 为“1性质函数”,求
为“1性质函数”,求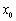 ;
;
(2) 判断函数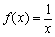 是否为“
是否为“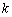 性质函数”?说明理由;
性质函数”?说明理由;
(3) 若函数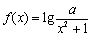 为“2性质函数”,求实数
为“2性质函数”,求实数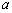 的取值范围;
的取值范围;
解:(1)由 得
得 ,… 2分
,… 2分 ,
, 。 4分
。 4分
(2)若存在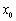 满足条件,则
满足条件,则 即
即 ,. 7分
,. 7分
 ,
, 方程无实数根,与假设矛盾。
方程无实数根,与假设矛盾。 不能为“k性质函数”。 10分
不能为“k性质函数”。 10分
(3)由条件得: , 11分即
, 11分即 (
( ,化简得
,化简得
 , 14分当
, 14分当 时,
时, ; 15分当
; 15分当 时,由
时,由 ,
,
 即
即 ,
, 。 …. 17分
。 …. 17分
综上, 。
。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
给出下列三个等式:f(xy)=f(x)+f(y),f(x+y)=f(x)f(y),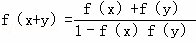 .下列函数中不满足其中任何一个等式的是( )
.下列函数中不满足其中任何一个等式的是( )
|
| A. | f(x)=3x | B. | f(x)=sinx | C. | f(x)=log2x | D. | f(x)=tanx |
 ,
, 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 的最大值为6,则
的最大值为6,则 ______.
______. ,则
,则 ______.
______. ,现有四个命题:
,现有四个命题: ,则
,则 ②若
②若
 ④若
④若
 的图象是
的图象是
 上
上 满足:
满足: ,当
,当 时,
时, ,则
,则 = .
= . 是函数
是函数 的零点,
的零点, ,则①
,则① ;②
;② ;③
;③ ;④
;④ 其中正确的命题是( )(A)①④ (B)②④ (C)①③ (D)②③
其中正确的命题是( )(A)①④ (B)②④ (C)①③ (D)②③ ” 的否定是“对任意的
” 的否定是“对任意的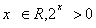 ”;
”;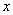 的不等式
的不等式 恒成立,则
恒成立,则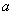 的取值范围是
的取值范围是 ;
;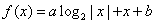 为奇函数的充要条件是
为奇函数的充要条件是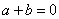 ;
;