题目内容
已知tan（
+α）=
．
（1）求tanα的值；
（2）求2sin2α+3sinαcosα-cos2α的值．
| π |
| 4 |
| 1 |
| 2 |
（1）求tanα的值；
（2）求2sin2α+3sinαcosα-cos2α的值．
考点：三角函数中的恒等变换应用
专题：三角函数的求值
分析：（1）首先，结合两角和的正切公式，直接解出tanα的值；
（2）利用（1），将所给的式子用tanα表示即可．
（2）利用（1），将所给的式子用tanα表示即可．
解答：
解：（1）∵tan（
+α）=
，
∴
=
，
∴tanα=-
．
（2）∵2sin2α+3sinαcosα-cos2α
=
=
=
=-
，
∴2sin2α+3sinαcosα-cos2α的值-
．
| π |
| 4 |
| 1 |
| 2 |
∴
| 1+tanα |
| 1-tanα |
| 1 |
| 2 |
∴tanα=-
| 1 |
| 3 |
（2）∵2sin2α+3sinαcosα-cos2α
=
| 2sin2α+3sinαcosα-cos2α |
| sin2α+cos2α |
=
| 2tan2α+3tanα-1 |
| tan2α+1 |
=
2×(-
| ||||
(-
|
=-
| 8 |
| 5 |
∴2sin2α+3sinαcosα-cos2α的值-
| 8 |
| 5 |
点评：本题重点考查三角公式，同角三角函数基本关系式等知识，属于中档题．
练习册系列答案
相关题目
已知向量
=（-2，1），向量
与
的夹角为180°，且|
|=2
，则
=（ ）
| β |
| α |
| β |
| α |
| 5 |
| α |
| A、（-4，2） |
| B、（4，-2） |
| C、（-4，-2） |
| D、（4，2） |
已知点A（a，b），B（x，y）为抛物线y=x2上两点，且x＞a，记|AB|=g（x）．若函数g（x）在定义域（a，+∞）上单调递增，则点A的坐标不可能是（ ）
| A、（1，1） |
| B、（0，0） |
| C、（-1，1） |
| D、（-2，4） |
某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数．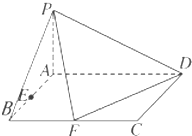
已知四棱锥P-ABCD的底面ABCD是矩形，PA⊥平面ABCD，AD=2，AB=1，E，F分别是线段AB，BC的中点，
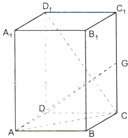如图，长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，G是CC1上的动点．