题目内容

已知向量
β
=（-2，1），向量
α
与
β
的夹角为180°，且|
α
|=2
5
，则
α
=（　　）
A、（-4，2）
B、（4，-2）
C、（-4，-2）
D、（4，2）
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：根据向量
β
=（-2，1），且向量
α
与
β
的夹角为180°，可设向量
α
=（-2x，x），x＜0；由|
α
|=2
5
，求出x的值，即得
α
．
解答： 解：根据题意，设向量
α
=（-2x，x），其中x＜0；
∵|
α
|=2
5
，
∴
(-2x)2+x2
=2
5
，
即5x2=20，
解得x=±2；
取x=-2，
∴
α
=（4，-2）．
故选：B．
点评：本题考查了平面向量的坐标运算问题，解题的关键是根据题意，设出向量
α
的坐标表示，是基础题．
练习册系列答案
相关题目
对于集合A={a1，a2…an} （n∈N*，n≥3），定义集合S={x|x=ai+aj，1≤i＜j≤n}，记集合S中的元素个数为S（A）．
（1）若集合A={1，2，3，4}，则S（A）=
 
．
（2）若a1，a2，…，an是公差大于零的等差数列，则S（A）=
 
（用含n的代数式表示）．
曲线f（x）=xlnx+2在点x=1处的切线方程为（　　）
A、y=2x+2
B、y=2x-2
C、y=x-1
D、y=x+1
已知向量
a
=（3，1），
b
=（1，3），
c
=（k，7），若（
a
-
c
）∥
b
，则k=（　　）
A、1B、3C、5D、7
设a＞0，b＞0，e是自然对数的底数，则（　　）
A、若ea-3b=eb-2a，则a＜b
B、若ea-3b=eb-2a，则a＞b
C、若ea+3b=eb+2a，则a＜b
D、若ea+3b=eb+2a，则a＞b
若双曲线
x2
a2
-
y2
b2
=1的一条渐近线方程为x+3y=0，则此双曲线的离心率为（　　）
A、
3
10
10
B、
10
3
C、2
2
D、
10
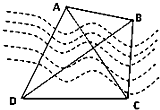如图，A、B两点都在河的对岸（不可到达），为了测量A、B两点间的距离，选取一条基线CD，A、B、C、D在一平面内．测得：CD=200m，∠ADB=∠ACB=30°，∠CBD=60°，则AB=（　　）
A、
200
3
3
m
B、200
3
m
C、100
2
m
D、数据不够，无法计算
如果执行如图的程序框图，输出的S=72，则判断框中为（　　）
A、k≥9B、k≤8
C、k≤9D、k≥8
已知tan（
π
4
+α）=
1
2
．
（1）求tanα的值；
（2）求2sin2α+3sinαcosα-cos2α的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网