题目内容
已知f(x)=sin(
+x)cosx-sinxcos(π-x).
(1)求函数f(x)的单调递增区间;
(2)在△ABC中,已知A为锐角,f(A)=1,BC=2,B=
,求AC边的长.
| π |
| 2 |
(1)求函数f(x)的单调递增区间;
(2)在△ABC中,已知A为锐角,f(A)=1,BC=2,B=
| π |
| 3 |
考点:正弦定理,三角函数中的恒等变换应用
专题:计算题,三角函数的图像与性质,解三角形
分析:(1)利用两角和公式和倍角公式对函数解析式化简,利用三角函数的性质求得函数的单调递增区间.
(2)先根据(1)中函数解析式和f(A)的值,求得A,进而根据正弦定理求得AC的长.
(2)先根据(1)中函数解析式和f(A)的值,求得A,进而根据正弦定理求得AC的长.
解答:
解:(1)f(x)=sin(
+x)cosx-sinxcos(π-x)
=cosxcosx+sinxcosx
=cos2x+
=
+
=
sin(2x+
)+
,
∴当2kπ-
≤2x+
≤2kπ+
,(k∈Z),
即-
+kπ≤x≤
+kπ时,函数单调增.
∴函数f(x)的单调递增区间为[-
+kπ,
+kπ](k∈Z)
(2)∵f(A)=
sin(2A+
)+
=1
∴sin(2A+
)=
,
∴2∠A+
=
或
∴∠A=0或
,
∵0<∠A<π
∴∠A=
∵
=
,
∴AC=
•sinB=
×
=
| π |
| 2 |
=cosxcosx+sinxcosx
=cos2x+
| sin2x |
| 2 |
=
| cos2x+1 |
| 2 |
| sin2x |
| 2 |
=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴当2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
即-
| 3π |
| 8 |
| π |
| 8 |
∴函数f(x)的单调递增区间为[-
| 3π |
| 8 |
| π |
| 8 |
(2)∵f(A)=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴sin(2A+
| π |
| 4 |
| ||
| 2 |
∴2∠A+
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴∠A=0或
| π |
| 4 |
∵0<∠A<π
∴∠A=
| π |
| 4 |
∵
| BC |
| sinA |
| AC |
| sinB |
∴AC=
| BC |
| sinA |
| 2 | ||||
|
| ||
| 2 |
| 6 |
点评:本题主要考查了正弦定理的应用和三角函数的基础知识.综合考查了诱导公式、两角和公式、倍角公式等基础知识.

练习册系列答案
相关题目
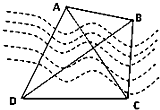 如图,A、B两点都在河的对岸(不可到达),为了测量A、B两点间的距离,选取一条基线CD,A、B、C、D在一平面内.测得:CD=200m,∠ADB=∠ACB=30°,∠CBD=60°,则AB=( )
如图,A、B两点都在河的对岸(不可到达),为了测量A、B两点间的距离,选取一条基线CD,A、B、C、D在一平面内.测得:CD=200m,∠ADB=∠ACB=30°,∠CBD=60°,则AB=( )A、
| ||||
B、200
| ||||
C、100
| ||||
| D、数据不够,无法计算 |
某校共有高中学生1000人,其中高一年级400人,高二年级340人,高三年级260人,现采用分层抽样抽取容量为50的样本,那么高一、高二、高三各年级抽取人数分别为( )
| A、20、17、13 |
| B、20、15、15 |
| C、40、34、26 |
| D、20、20、10 |