题目内容
10.一个几何体的三视图如图所示,则这个几何体是( )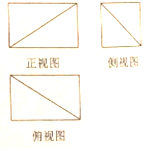
| A. | 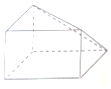 | B. | 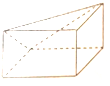 | C. | 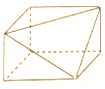 | D. | 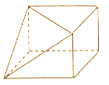 |
分析 分析给定四个答案中的几何体三视图的形状,可得结论.
解答 解:A中几何体的正视图中应该画矩形的另一条对角线,且是虚线,故A错误;
(B)中几何体的正视图中的对角线应该是虚线,故B错误;
C中几何体的正视图中的对角线应该是另一条,故C错误.
故选:D
点评 本题考查的知识点是简单几何体的三视图,难度不大,属于基础题.

练习册系列答案
相关题目
20.若函数f(x)是定义在R上的奇函数,但当x>0时,f(x)=$\frac{1}{x+1}$-log2(x+1),则满足4f(x+1)>7的实数x的取值范围是( )
| A. | (2,+∞) | B. | (-∞,-1)∪(3,+∞) | C. | (-4,2) | D. | (-∞,-4) |
1.直线y=mx+1与曲线x=2+$\sqrt{1-{y}^{2}}$的图象始终有交点,则m的取值范围是( )
| A. | (-1,0) | B. | [-1,0] | C. | (-1,-$\frac{1}{3}$) | D. | [-1,-$\frac{1}{3}$] |
5.已知N是自然数集,在数轴上表示出集合A,如果所示,则A∩N=( )
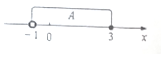

| A. | {-1,0,1,2,3} | B. | {0,1,2,3} | C. | {1,2,3} | D. | {2,3} |
19.若△ABC的三个内角满足tanAtanBtanC>0,则△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 任意三角形 |
20.下面使用类比推理正确的是( )
| A. | 由实数运算“(ab)t=a(bt)”类比到“($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$)” | |
| B. | 由实数运算“(ab)t=at+bt”类比到“($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•$\overrightarrow{c}$+$\overrightarrow{b}$•$\overrightarrow{c}$” | |
| C. | 由实数运算“|ab|=|a||b|”类比到“|$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|” | |
| D. | 由实数运算“$\frac{ac}{bc}$=$\frac{a}{b}$”类比到“$\frac{\overrightarrow{a}•\overrightarrow{c}}{\overrightarrow{b}•\overrightarrow{c}}$=$\frac{\overrightarrow{a}}{\overrightarrow{b}}$” |