题目内容
2.在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρcos2θ=2sinθ,它在点$M(2\sqrt{2},\frac{π}{4})$处的切线为直线l.(1)求直线l的直角坐标方程;
(2)已知点P为椭圆$\frac{x^2}{3}+\frac{y^2}{4}$=1上一点,求点P到直线l的距离的取值范围.
分析 (1)利用极坐标方程与普通方程的互化求解即可.
(2)设出椭圆的参数方程,利用点到直线的距离公式化简求解即可.
解答 (本小题满分10分)
解:(1)∵曲线C的极坐标方程为ρcos2θ=2sinθ,
∴ρ2cos2θ=2ρsinθ,
∴曲线C的直角坐标方程为y=$\frac{1}{2}$x2,
∴y′=x,又M(2$\sqrt{2}$,$\frac{π}{4}$)的直角坐标为(2,2),
∴曲线C在点(2,2)处的切线方程为y-2=2(x-2),
即直线l的直角坐标方程为:2x-y-2=0. …(5分)
(2)P为椭圆$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{4}=1$上一点,设P($\sqrt{3}$cosα,2sinα),
则P到直线l的距离d=$\frac{|2\sqrt{3}cosα-2sinα-2|}{\sqrt{5}}$=$\frac{|4sin(α-\frac{π}{3})+2|}{\sqrt{5}}$,
当sin(α-$\frac{π}{3}$)=-$\frac{1}{2}$时,d有最小值0.
当sin(α-$\frac{π}{3}$)=1时,d有最大值$\frac{6\sqrt{5}}{5}$.
∴P到直线l的距离的取值范围为:[0,$\frac{6\sqrt{5}}{5}$].…(10分)
点评 本题考查椭圆的参数方程,极坐标方程与普通方程的互化,点到直线的距离公式的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
12.函数f(x)=(kx+4)lnx-x(x>1),若f(x)>0的解集为(s,t),且(s,t)中只有一个整数,则实数k的取值范围为( )
| A. | ($\frac{1}{ln2}$-2,$\frac{1}{ln3}$-$\frac{4}{3}$) | B. | ($\frac{1}{ln2}$-2,$\frac{1}{ln3}$-$\frac{4}{3}$] | C. | ($\frac{1}{ln3}$-$\frac{4}{3}$,$\frac{1}{2ln2}$-1] | D. | ($\frac{1}{ln3}$-$\frac{4}{3}$,$\frac{1}{2ln2}$-1) |
10.一个几何体的三视图如图所示,则这个几何体是( )
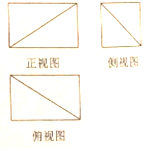

| A. | 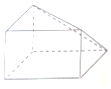 | B. | 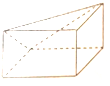 | C. | 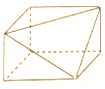 | D. | 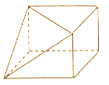 |
7.i是虚数单位,若复数z满足zi=-1+i,则复数z的共轭复数是( )
| A. | 1-i | B. | 1+i | C. | -1+i | D. | -1-i |
11.圆x2+(y-1)2=4上点到曲线f(x)=-x3+3x2在点(1,f(1))处的切线的最远距离为( )
| A. | $\frac{\sqrt{10}}{4}$ | B. | $\frac{10+\sqrt{10}}{5}$ | C. | $\frac{10-\sqrt{10}}{5}$ | D. | $\frac{10+2\sqrt{10}}{5}$ |
12.要得到函数y=sin ($\frac{π}{4}$-$\frac{x}{2}$)的图象,只需将y=cos $\frac{x}{2}$的图象( )
| A. | 向左平移$\frac{π}{2}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |