题目内容
1.直线y=mx+1与曲线x=2+$\sqrt{1-{y}^{2}}$的图象始终有交点,则m的取值范围是( )| A. | (-1,0) | B. | [-1,0] | C. | (-1,-$\frac{1}{3}$) | D. | [-1,-$\frac{1}{3}$] |
分析 直线y=mx+1恒过C(0,1)点,曲线x=2+$\sqrt{1-{y}^{2}}$ 知x≥2,且可转化为:(x-2)2+y2=1 (x≥2),利用数形结合即可求解.
解答 解:由题意知:直线y=mx+1恒过C(0,1)点;
曲线x=2+$\sqrt{1-{y}^{2}}$ 知x≥2,且可转化为:(x-2)2+y2=1 (x≥2),
即以(2,0)为圆心,半径R=1的半圆; 
由图知:A(2,1),B(2,-1);
kBC=$\frac{1-(-1)}{0-2}$=-1;kAC=0;
故m的取值范围为[-1,0]
故选:B
点评 本题主要考查了直线与圆的位置关系与交点,利用数形结合与斜率知识点,属中等题.

练习册系列答案
相关题目
11.设F1(-c,0),F2(c,0)是椭圆C1:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)与双曲线C2有公共焦点F1、F2,(F1、F2分别为左、右焦点),它们在第一象限交于点M,离心率分别为e1和e2,线段MF1的垂直平分线过F2,则$\frac{{{e_2}-{e_1}}}{{{e_1}{e_2}}}$的值为( )
| A. | $2\sqrt{2}$ | B. | $3\sqrt{2}$ | C. | 3 | D. | 2 |
12.函数f(x)=(kx+4)lnx-x(x>1),若f(x)>0的解集为(s,t),且(s,t)中只有一个整数,则实数k的取值范围为( )
| A. | ($\frac{1}{ln2}$-2,$\frac{1}{ln3}$-$\frac{4}{3}$) | B. | ($\frac{1}{ln2}$-2,$\frac{1}{ln3}$-$\frac{4}{3}$] | C. | ($\frac{1}{ln3}$-$\frac{4}{3}$,$\frac{1}{2ln2}$-1] | D. | ($\frac{1}{ln3}$-$\frac{4}{3}$,$\frac{1}{2ln2}$-1) |
10.一个几何体的三视图如图所示,则这个几何体是( )
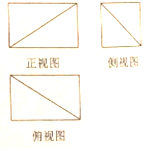

| A. | 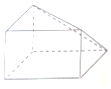 | B. | 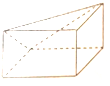 | C. | 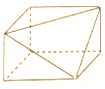 | D. | 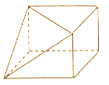 |
11.圆x2+(y-1)2=4上点到曲线f(x)=-x3+3x2在点(1,f(1))处的切线的最远距离为( )
| A. | $\frac{\sqrt{10}}{4}$ | B. | $\frac{10+\sqrt{10}}{5}$ | C. | $\frac{10-\sqrt{10}}{5}$ | D. | $\frac{10+2\sqrt{10}}{5}$ |