题目内容
15.若一个幂函数和一个指数函数图象的一个交点是(2,4),则它们图象的另一个交点为(4,16).分析 分别设出指数函数和幂函数的解析式,求出即可.
解答 解:设幂函数为y=xa,则2a=4,解得:a=2,
可知幂函数为y=x2,
设指数函数为y=ax,则a2=4,解得:a=2,
故指数函数为y=2x,
由$\left\{\begin{array}{l}{y{=x}^{2}}\\{y{=2}^{x}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=16}\end{array}\right.$
所以它们图象的另一个交点是(4,16),
故答案为:(4,16).
点评 本题考查了求幂函数和指数函数的解析式,考查解方程组问题,是一道基础题.

练习册系列答案
相关题目
3.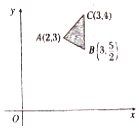 如图,已知点(x,y)在△ABC所包围的阴影部分区域内(包含边界),若B(3,$\frac{5}{2}$)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
如图,已知点(x,y)在△ABC所包围的阴影部分区域内(包含边界),若B(3,$\frac{5}{2}$)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
 如图,已知点(x,y)在△ABC所包围的阴影部分区域内(包含边界),若B(3,$\frac{5}{2}$)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
如图,已知点(x,y)在△ABC所包围的阴影部分区域内(包含边界),若B(3,$\frac{5}{2}$)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )| A. | [-$\frac{1}{2}$,+∞) | B. | [0,+∞) | C. | (-∞,-$\frac{1}{2}$] | D. | [-$\frac{1}{2}$,0] |
10.一个几何体的三视图如图所示,则这个几何体是( )
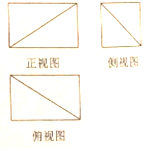

| A. | 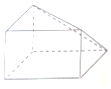 | B. | 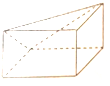 | C. | 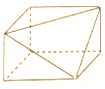 | D. | 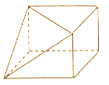 |
7.i是虚数单位,若复数z满足zi=-1+i,则复数z的共轭复数是( )
| A. | 1-i | B. | 1+i | C. | -1+i | D. | -1-i |
 (理科)如图,已知四棱锥P-ABCD的底面ABCD为菱形,且∠ABC=60°,AB=PC=2,PA=PB=$\sqrt{2}$,
(理科)如图,已知四棱锥P-ABCD的底面ABCD为菱形,且∠ABC=60°,AB=PC=2,PA=PB=$\sqrt{2}$,